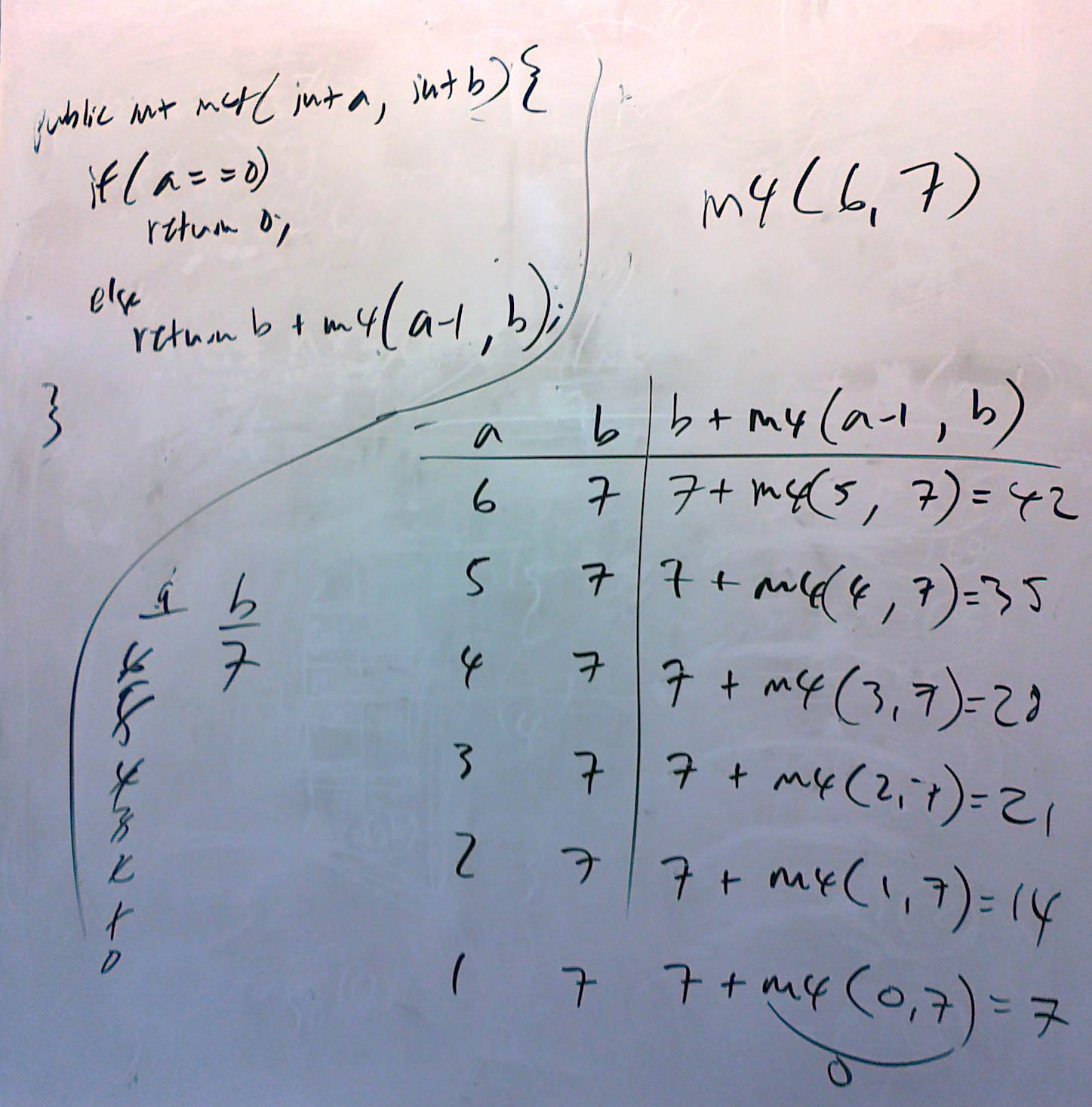
D.4.4
Trace recursive algorithms.
Teaching Note:
All steps and calls must be shown clearly.
LINK Connecting computational thinking and program design.
Sample Question - FORMER CURRICULUM - Not so much tracing, but a good overall recursive question.:
Given a program which functions like a linked list and has a recursive count method (HL 2 May 2008, question 1):
(e) State the name of the programming technique used in the countUp method used
in the List class. [1 mark]
To use this method the following statement is used.
output(list.count());
(f) State the sequence of steps that flow from executing the above statement and
state clearly how the count method stops executing. [4 marks]
Sample Question - FORMER CURRICULUM:
Consider the following recursive algorithm.
int recur(int b){
if (b==0)
return 1;
else
return 2*recur(b-1);
}
(a) State two features of a recursive algorithm. [2 marks]
(b) State the value returned if the method is called by recur(3). [2 marks]
JSR Notes:
CodingBat.com for lots of good exercises.
These below, from a textbook I used to use tea=============ching AP CS, by Leon Schramm.
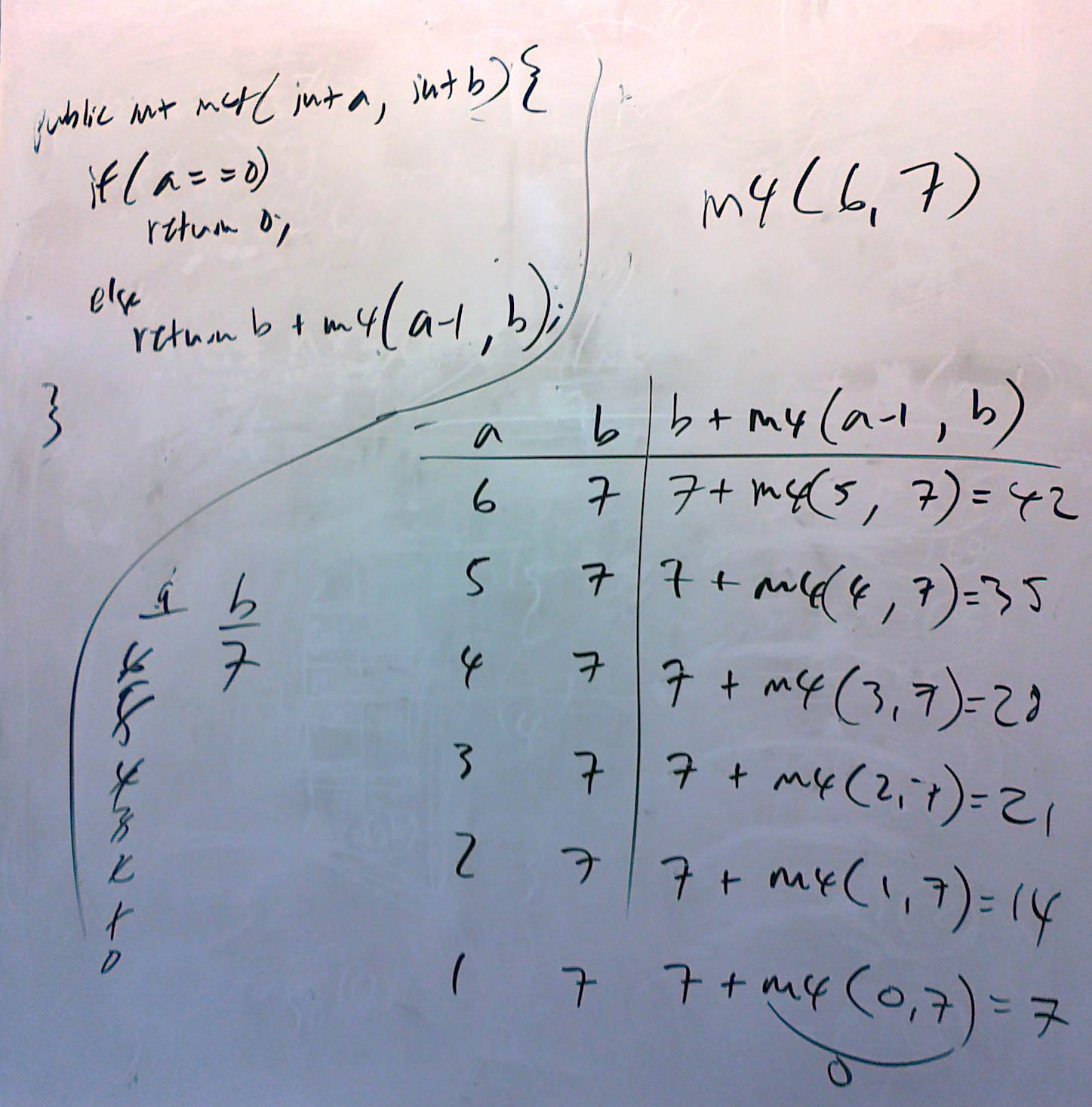
Above is an image of the tracing exercise m4.
And here is a video showing how to do the tracing exercise m5 below:
The idea is that when the first instance of the recursive method is called, the if condition is not true, so the method goes to the else block, in which another instance of the method is called. We show that in the trace table above as the call of m4(6, 7) is 7 + m4(5, 7). But we don't know what m4(5.7) is, since the "a" variable is still not 0. So another call to the m4 method is required, and so on, until, finally variable "a" is indeed 0, from which point we can work on up through the "stacked" calls.
public int m1(int n) // m1(6)
{
if (n == 1)
return 25;
else
return n + m1(n-1);
}
public int m2(int n) // m2(5)
{
if (n == 5)
return 0;
else
return n + m2(n+1);
}
public int m3(int n) // m3(6)
{
if (n == 1)
return 1;
else
return n * m3(n-1);
}
public int m4(int a, int b) // m4(6,7)
{
if (a == 0)
return 0;
else
return b + m4(a-1,b);
}
-------------------------- Similar straigt-fowrard exercises continued below
Factorial try: factorial(5)
public static int factorial(int n){
if(n == 1){
return 1;
}else{
return n * factorial(n - 1);
}
}
Fibonacci Sequence try: fibonacci(6)
public static int fibonacci(int n){
if(n == 0 || n == 1){
return n;
}else{
return fibonacci(n - 1) + fibonacci(n - 2);
}
} There are two ways you can approach coming to the solution of a two recursive call in one line problem. One, showing the tree structure, and the other a regular trace table. Both seen below.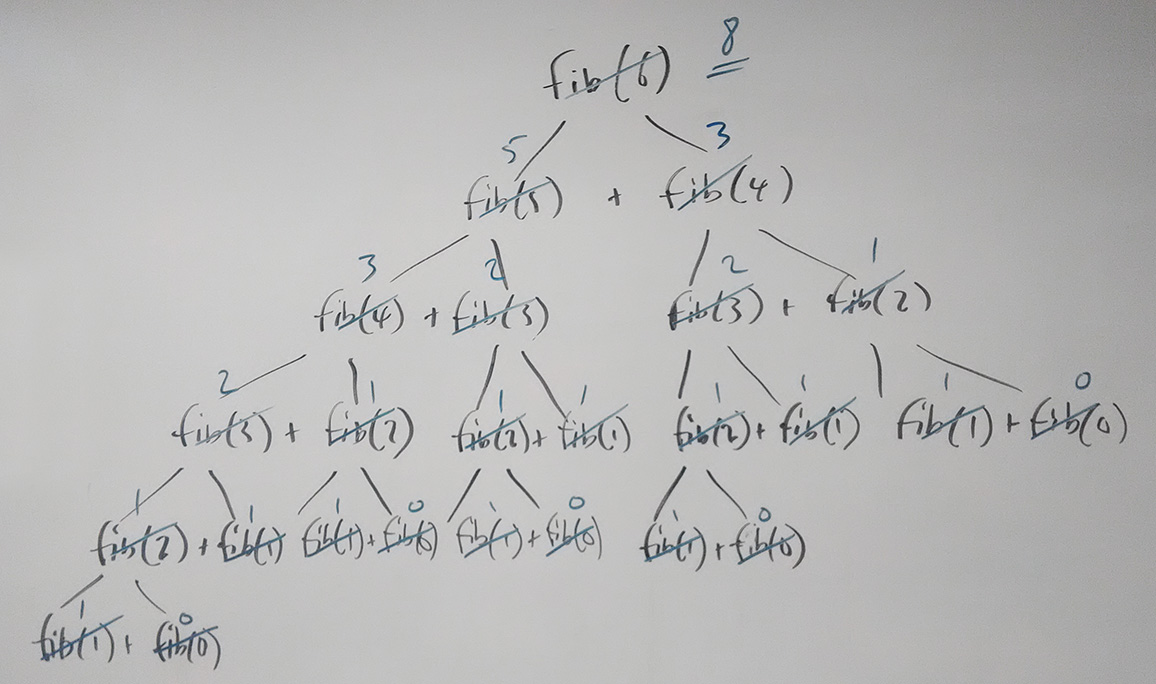

Recursive Binary Search try the following array:
45 62 64 71 75 83 88 89 94 101 112 145 152
and searching for 89
Note that practically you have to "kick-start" a recursive binary search with a
helper function, so just assume the array above sent, along with 0, 12, 145
public static int recursiveBinarySearch(int[] arr, int low, int high, int key) { if (low < high) { int mid = low + high/ 2; if(k == arr[mid]{ return mid; else if (key < arr[mid]) { return recursiveBinarySearch(arr, low, mid-1, key); // so high sent as mid - 1 } else { //i.e. key > arr[mid] return recursiveBinarySearch(arr, mid+1, high , key); // so low sent as mid + 1 } } return -1; }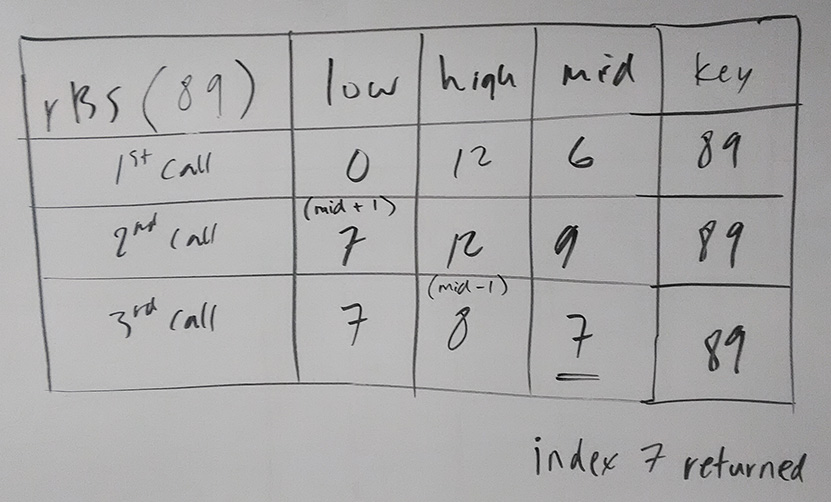
-------------------------- Continuation of similar straight-forward exercises from above
public int m5(int a, int b) // m5(5,3) { if (a == 0) return 1; else return b * m5(a-1,b); } public int m6(int a, int b) // m6(3,5) { if (b == 0) return 1; else return a * m6(a,b-1); } public int m7(int a, int b) // m7(7,3) { if (a < b) return 5; else return b + m7(a-1,b+1); } public int m8(int n) // m8(6) { if (n == 1 || n == 0) return 0; else return n + m8(n-1) + m8(n-2); //So this will require branching tracing }
Make sure you look at both of these examples, and the hints for understanding them in-between.
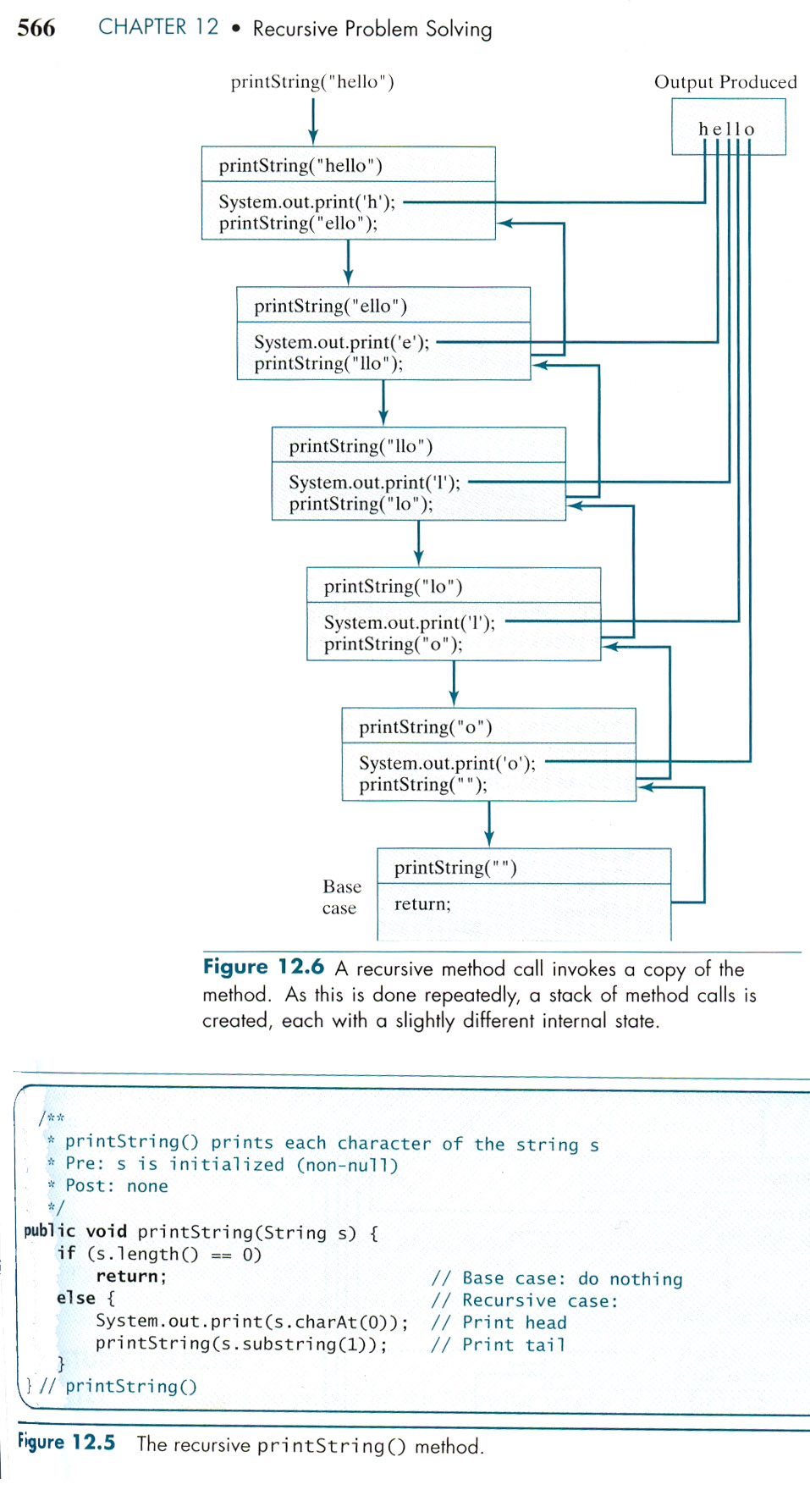
Hints for understanding and following both of these, above and below:
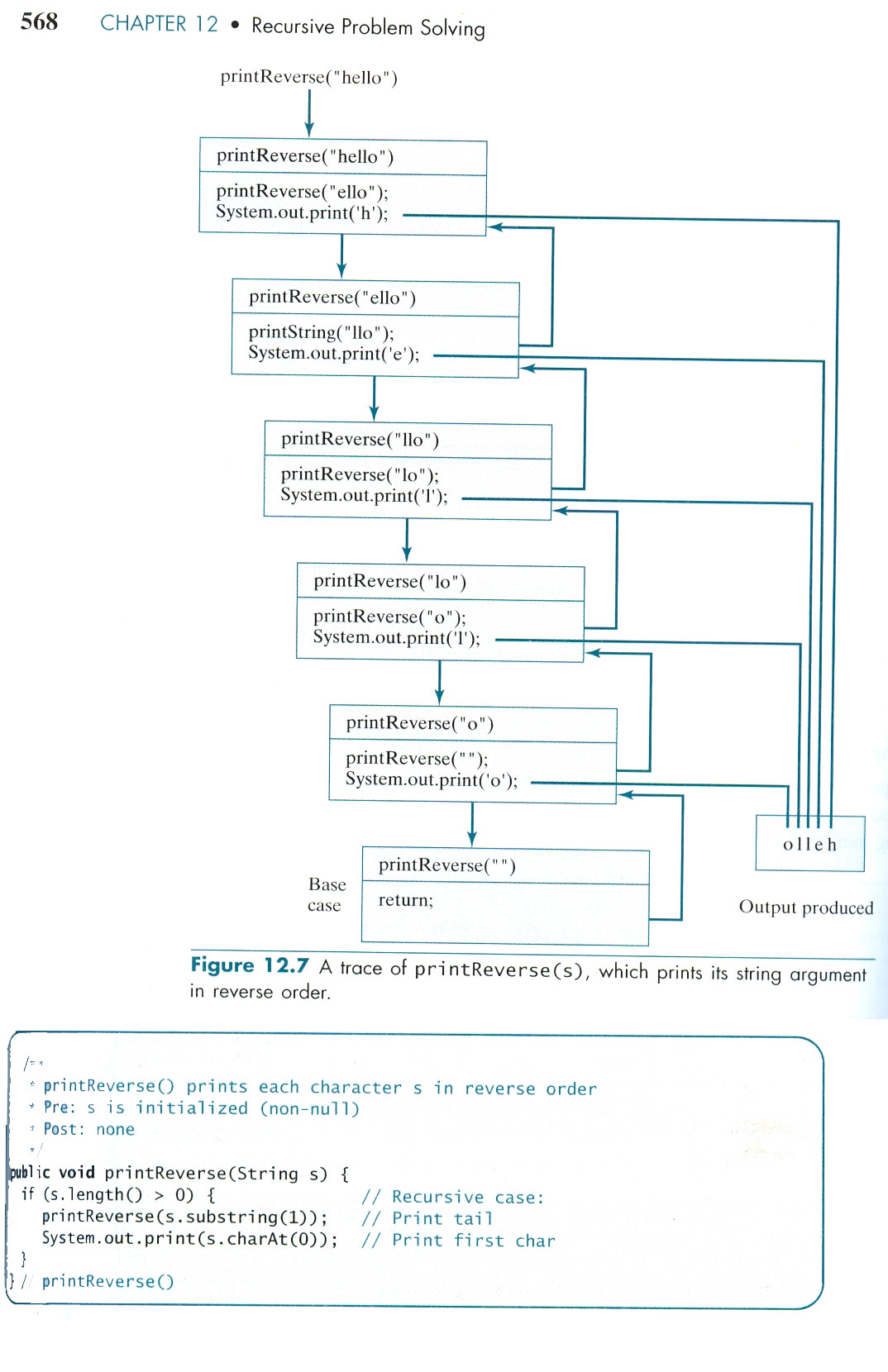
- The difference between the two methods is mainly because of the order in which the printing out of the letter and the recursive call are made.
- In the diagram, each lower block is the instance of the method that was called in the block above.
- A method is not finished until you get to (in the diagram) its final semi-colon.
- In recursion, the methods that call other methods recursively are not out of memory until those that it called are finished; they are placed on a stack of unfinished methods.
- It is the interruption of the recursive calls which is the secret to how things work.
- In the code, recall that the charAt() method of the String class prints out the character at a certain element number. So for the String "hello world", charAt(7) would print return 'w'.