Sample Question:

From Sample Paper 1 2014:

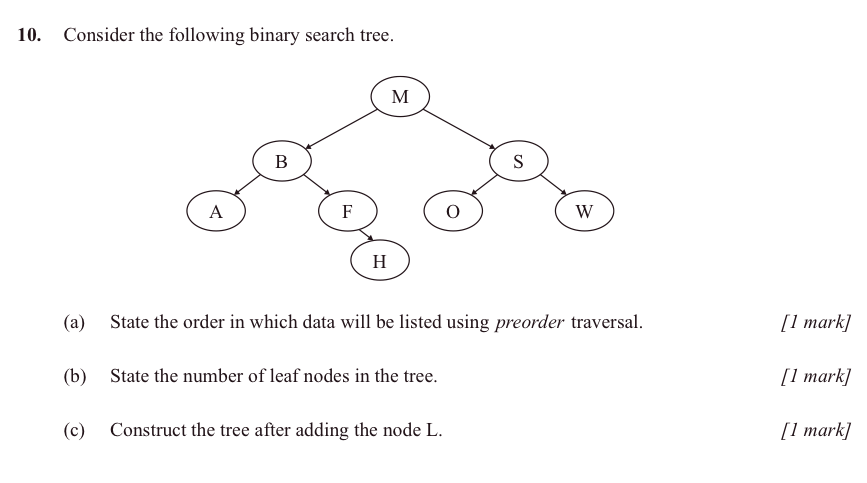
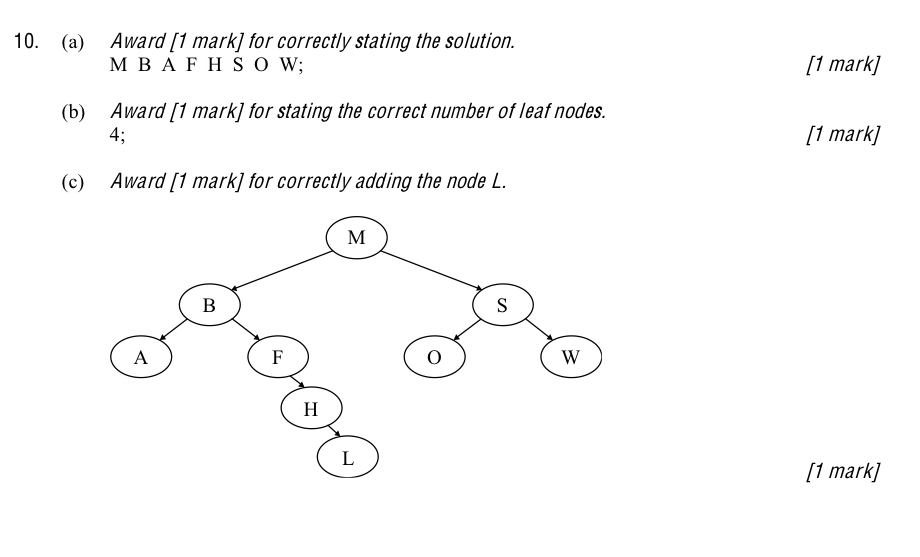
JSR Notes:

In-order, pre-order and post-order are the three main ways to traverse a binary tree. The idea is that we want to "traverse" the tree, thereby going to each and every node. And the question is how will we do so? We cannot just "start at the beginning" and "go to the end" as we would be able to do with an array or with a list. It's more difficult to figure out how to traverse because each node (except for the end leafs) has two ways you can go. An iterative solution does not lend itself to this sort of situation, but a recursive one does: at each node, visit its children a certain way.

To remember which order is which, "in-order", "pre-order" and "post-order" think of when the node itself is dealt with each time; is it dealt with first? that's "pre", is it dealt with last? that's "post", or is it dealt with "in-order", the left, then it, then the right..

• With pre, the node itself is dealt with first
• With post, the node itself is dealt with last
• And in-order, the node itself id dealt with in-between the left and right.

And left is before right - think of soldiers marching: "left, left, left, right, left..."

So with pre-order, we:
- visit the node itself ("node is often written as "root"")
- visit the left node
- visit the right node

With in-order, we:
- visit the left node
- visit the node itself
- visit the right node

And with post-order, we
- visit the left node
- visit the right node
- visit the node itself

This may be, in fact, all that is required for this assessment statement: to state the order in which one or all of the traversals operate.

But the more involved question that can be asked is to trace the traversal of an actual tree - and this is more what this assessment statement is getting at: "State the result of inorder, postorder and preorder tree traversal." The question is actually is this more a Topic 5 question, or OOP Option - it could come from 5.1.3, or this, 5.1.16, or indeed from D.4.4. I'd say it's most likely to be a "Topic 5 question", and so Paper 1 - but be prepared with the ability to do it on both Paper 1 and Paper 2.

For your deeper understanding, here's the detailed animation of one of them. But this should be a bit beyond what you need to know, and you would not be asked to trace, explicitly, the way the animation does.

animation of Binary Tree traversal trace

And here's another VERY GOOD video. I like the way the guy adds "V" for value, or "R" for Right, and "L" for Left when as each of those things is done. So watch it first, and pretend I did that too in my video below, rather than just saying it.

Pre-order, In-order, and Post-order Traversals of Binary Trees

psvm{
        System.out.println(traverseInOrder(studentTree, ""); 
        //assume a binary tree of Student objects, called studentTreemade, made before this
}
private String traverseInOrder(StudentNode p, String inOrderString){ // 'p' chosen for "pointer"
    if(p != null){
        traverseInOrder(p.getLeft(), inOrderString);
        inOrderString += p.getValue().getName();
        traverseInOrder(p.getRight(), inOrderString);
    }
    return inOrderString;
}

Pre-order Traversal:

(backup of video)

In-order Traversal:

(backup of video)

Post-order Traversal:

(backup of video)