Sample Question:

sdfsdfsf

JSR Notes:

 

Images needed!

 

Compression of Data

Compression of data is a process of somehow making the size of a file, or a directory of files, less than its full, uncompressed size.

User-level Compression

A common user-level compression format you may be familiar with is .zip. A Mac can compress to this format by default in the Finder. Just right-click/Ctrl-click on any file or folder, and go "Compress", and you end up with a .zip version of that file or folder, which will be less size in terms of bytes.

Other compressed file types that you might run across include:

• .jpeg and .gif for images,
• .mp3 for audio files,
• .mp4 for video files,
  
• .jar for Java files,
  
• .dmg for Mac install files,
  
• .tar and .rar, which are also for file archiving.
  

The main goal of all these user-level compressed formats is to make files and folders smaller, so they take up less memory.

- Multimedia User-level Compression

For multimedia compressed files, like jpegs and mp3s, the files can be used/played in the compressed form, though often with a loss of quality compared to the uncompressed versions. This compression is useful because firstly it means that more images or music can be stored on a particular device, which has, by definition limited storage space. And more to the point of this assessment statement, the files can travel more quickly across networks, since they are smaller in size.

- Archiving User-level Compression

Meantime, with all the other "archive" type compressed formats, like .rar, and .zip, the compressed files cannot be used as-is; rather they have to be uncompressed to be used. Their purpose in compressed form is simply to archive the file/folder so that it takes up less space. When we want to use files/folders that have been archived, we temporarily "un-zip" them, and use them. And then, when we are finished using them, we may choose to re-zip them, and trash the unzipped version.

A pdf compressed in the Finder of a Mac, with CTRL-click, Compress"

Network-level Compression

All of such "every-day" use of compression discussed above is different from having compression as part of a networking protocol, implemented by devices such as routers and switches. The idea with network-level compression is that each and every packet/frame that is sent, or sent on, by a piece of networking hardware is compressed (or futher compressed) to ready it for network transmission, regardless of whether the original form of the data was compressed or not.

Data compression reduces the size of data frames to be transmitted over a network link. (Frames are similar to packets, but at a lower level of the OSI model; the data link layer.) A particular kind of network data compression will use a certain algorithm at the transmission end, and a complementary algorithm at the receiving end. The compression algorithm somehow is able to remove data from the frames on the sending side of the link, and then is able to have that data replaced correctly at the receiving side. Because the condensed frames take up less bandwidth, a greater volume of data is transmitted per unit of time. Network compression therefore allows information to be transmitted and disseminated more rapidly.

Network Compression is Lossless

When talking about compression of multimedia files (like jpegs and mp3s) we often talk about "lossy" vs. "lossless" conversion techniques. With lossy, some of the original quality is lost (see more about this below). But in the case of network connection, every single bit which is sent needs to be able to be reproduced where it is received, so all network compression needs to be lossless. The two most commonly used compression algorithms on internet devices are the Stacker compression and the Predictor data compression.

Redundant data replaced by tokens

These algorithms are network-compression level compression, but they share the same general approach of other compression in that they look for redundant data, and replace it with smaller "tokens". So if the same 1024 bit pattern, for example, is repeated a dozen times, then after the first time, every other time it is repeated, a token of only 128 bits, let's say, representing it can be sent in its place. See more about this, if you wish, below, or see actual technical details at this link.

Generally, Why Network Compression of Data is Necessary

Note that the assessment statement uses the word "necessary". Why is compression necessary? Well, it's nice to download your file in half the time, but in terms of being necessary, you should be thinking about the macro view of the overall network. Any given network reaches a point where it is simply impractical to use due to speed issues and congestion, resulting from too much traffic. So one of the ways to keep the network practically useful is to somehow limit the amount of data being transmitted. And one great way to do that is to have compression of data, both by users compressing files before transmission, and also having compression of all frames done at the network transmission level.

"Dissemination of Information More Rapidly" & Cloud Computing

The other thing to note in the Teaching Note is the idea of disseminating information more rapidly. This hints at the direction the Internet and data/application distribution is heading currently. Companies, in particular, are keen to introduce and expand the "cloud" model of computing, in which they keep control of not only all data, but all applications. And so not only is data to be stored in various "clouds" (actually mega warehouses with thousands of servers), but also when users run an application (for example Word or Photoshop), they are actually running it across the Internet from the "cloud" (this is called SaaS - Software as a Service).

This means there are massive amounts of information moving back and forth across the Internet, and it means the more techniques that can be used for limiting and controlling that amount of information the better. Compression is one of these techniques.

 

Conclusion

In fact, both user level compression of files to be disseminated via networks, and network-level compression technologies, are options for speeding up network transmission rates world wide - they are relatively easy techniques to employ, and they yield results in a direct way.

To take an user-level compression example, at a certain transmission speed - say 8 Mbps (Megabits per second), which is about the worldwide average in 2018, a 100 Megabyte file (that's 800 Megabits) would take 100 seconds to be downloaded. If that file were compressed to half its size (50 Megabytes), then it would take half the time to download, i.e. 50 seconds.

So back to the assessment statement, simply put, compression of data is often necessary when transmitting across a network because with ever increasing amounts of data being transmitted, anything that speeds up that transmission should be employed.

 

 

 

 

---------------- ADDITIONAL INFORMATION BEYOND THE ASSESSMENT STATEMENT, BUT INTERESTING -------

 

So in terms of compression techniques, though not referred to directly in the assessment statement or the Teaching Note, you kinda have to have an idea of what they are, I think. So don't take too much time with what follows, but do have a general understanding of compression algorithms/techniques.

Lossy vs. Lossless

First of all you should realize that there are two possible results of compression, in terms of the loss of information. In lossy compression techniques, data is indeed lost through the compression. When expanded, the original file does not contain all of its original data. In the case of lossless compression techniques, upon expansion after compression, the file is back to it's original state; no data at all is lost (thus the term "lossless").

Image Compression

A photograph taken by a digital camera can be Megabytes and Megabytes. For under $100 (2019) you can buy a camera which takes 20 Mega pixel pictures. So at full quality, uncompressed, 24 bit color (refer to 2.1.10), that's 20 million x 3 bytes, or 60 Megabytes for one snap shot of your friends making faces at each other on the weekend. That's a lot of memory for something that does not have to be perfect quality - which is actually useful if you are going to zoom way in and work with it in Photoshop, for example. So it can be saved in several compressed formats, including GIF and JPEG.

With GIF compression, series of pixels that are the exact same color are found and recorded. So, say there are 20 white pixels in a row, the file will not save 20 three-byte (assuming 24 bit color) pieces of information (60 bytes in total), rather it will record the number of white pixels in a row; that makes the calculation three bytes for the color (the RGB value), and then, two bytes to store the number (5 bytes in total). See pages 178-181 of the yellow and red text book for a discussion of this, with a good set of diagrams. This is a lossless kind of compression.

With JPEG compression, (basically) square regions of an image are turned into gradients, whose mathematical representations are stored, rather than all the pixel information of each individual pixel. So, from one corner of a region which is dark brown, to the opposite corner which is light brown, the colors of in-between browns are distributed. There's lots more to it than this, but you get the idea. This is a lossy means of compression, as you are losing the actual pixel information; it is replaced by the various gradients. But zoomed out, and done in a limited way (choosing jpeg high quality when compressing), it can be hard to see the difference.

Recall me being zoomed in on a Photoshop image when saving as jpeg, and seeing, live, the gradients appearing.

The most common uncompressed image format (which, therefore saves each and every pixel) is TIFF.

--> See Photoshop Save for Web

Audio Compression

With digital audio, the most common uncompressed format is AIFF. It uses the "CD standard" of 44,100 samples per second and 16 bit sample size (or bit depth). So this means that each sample is the sound frequency that exists for a 1/44,100 fraction of a second, and each sample can be one of 65, 536 (2 ^ 16) frequencies.

So each second of an AIFF is 16 bits (2 bytes) x 44,100, or 88,200 bytes. A 3:00 minute single on the radio would thus be 180 seconds x 88,200 bytes, or 15 Megabytes x 2, because it's actually two channels (i.e. stereo), so 30 Megabytes. And from your personal experience you know that an average (compressed) mp3 is only about 3 Megabytes, so that's lots of compression.

To save time, I'm going to copy and paste images from the Internet, but will replace them with my own diagram some time:

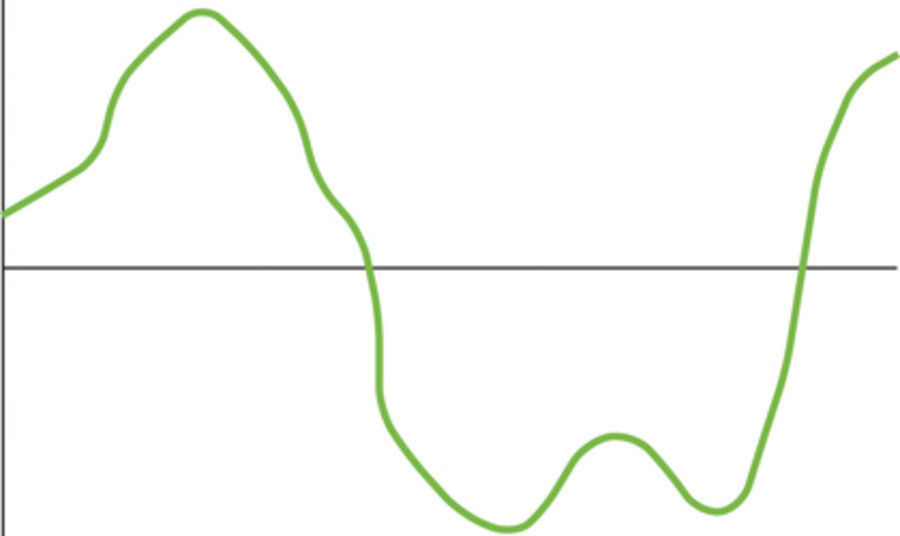
Sound wave (analogue - i.e. continuous change in frequency - an infinite number of points along it.)

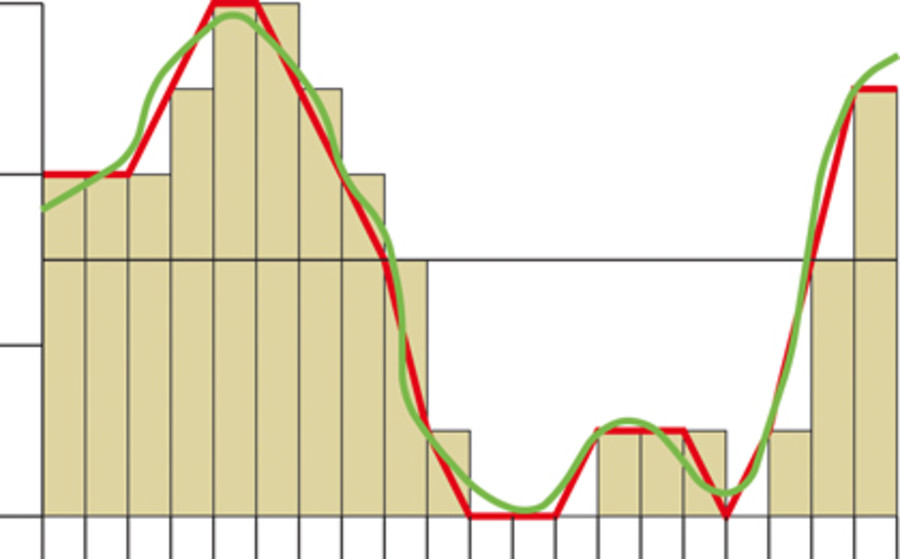
Digital sampling of that sound wave.

Compression could be done in a lossless, similarly to GIF, by finding groups of exactly the same samples. So in this diagram there are two groups of three. To be efficient, you would be looking for more in a row than this, but you get the idea.

A lossy audio compression technique (such as MP3) could be a lot "rougher" and look for groups of samples that are close to each other, and then save that group as all the same frequency. (So from sample # 27,123 in second 44, to sample # 27,300 in second 44, digitally save frequency 17.125 kHz - whereas in the uncompressed file, there would be a lot of variation in those 77 samples.)

 

Libor reports that the difference between full .wav to .mp3 is 10 to 1. So you have lost a great deal of information and fidelity.

Audio mastering is now done at 24 bit and 96 kHz. A 24 bit range of sound would mean 16,000,000 different pitches possible.