2.1.10
Outline the way in which data is represented in the computer.
Teaching Note:
To include strings, integers, characters and colours. This should include considering the space taken by data, for instance the relation between the hexadecimal representation of colours and the number of colours available.
TOK, INT Does binary represent an example of a lingua franca?
S/E, INT Comparing the number of characters needed in the Latin alphabet with those in Arabic and Asian languages to understand the need for Unicode.
Sample Question:
sdfsdfsf
JSR Notes:
This is actually a HUGE question to really understand it, but ultimately only one little assessment statement, so the way I'll approach it is with three "tiers", and four questions.
Orgainization of this notes page # 1: "Tiers"
In class, for instruction, the order of what follows may need to be mixed up a bit - going deeper and coming back to the "canned answers". But for study (since there's so much here), if you can understand the top tier, and are able to write the same sort of answer in your own words, you're good to go; otherwise, keep on reviewing on down through the notes.
- Tier 1: the actual "canned" summary information you will need for an IB exam question
- Tier 2: the teaching notes themselves tweaked out a little further
- OPTIONAL Tier 3: more full explanations to possibly help your understanding (bottom of this page)
And all of this we will divide up into four "Questions" as follows, that come verbatim from this assessment statement and teaching notes::
The 4 Likely IB Exam Questions
Q-A: "Outline the way in which data is represented in the computer", and " include strings, integers, characters and colours.
Q-B: (Discuss) "the space taken by data, for instance the relation between the hexadecimal representation of colours and the number of colours available."
Q-C: "Compare the number of characters needed in the Latin alphabet with those in Arabic and Asian languages to understand the need for Unicode."
Q-D: "Does binary represent an example of a lingua franca?"
____________________________________
Q-A Data Representation
Tier 1
Q-A: "Outline the way in which data is represented in the computer", and "include strings, integers, characters and colours.
Overall Answer - All data is represented on a computer in a binary way. In the RAM of a computer this binary representation is in the form of open circuits (the 1s of the binary code) and closed circuits (the 0s of the binary code). On hard drives, the binary representation is in the form of little regions that have one level of magnetism or another.
So all data, be they numeric data or color data or whatever, ultimately have to be able to be translated into a binary form. And for each particular kind of data, there are internationally agreed upon code sets of that match up particular numbers/characters/sounds/colors to binary numbers.
Integers
Integers are able to be stored simply as the binary equivalent of their decimal value. So the decimal number 6, in an 8-bit integer context would be 0000 0110. But usually, integer data types are "signed", meaning that they can represent positive or negative numbers. This is achieved by having the Most Significant Bit (the MSB) being a negative value, which, the way that additional places in a number system work, will be equal to the total positive value represented by the rest of the bits.
For example, for an 8-bit signed integer 1000 0000 is -128, and 0111 1111 is +127.
(Which would make 1111 1111 to be -128 + 127, or -1)
or for a 16-bit signed integer, 1000 0000 0000 0000 is - 32 768, and 0111 1111 1111 1111 is +32 767.
(And, again, 1111 1111 1111 1111 would be -1)
Characters
Each specific character (for example, 'A', 'g', '!', '#') in a given character set has an equivalent binary code. In the ASCII character set, for example, 'A' is represented by the following 8-bit binary number: 0100 0001.
Note that since both characters and integers share certain binary equivalents, they can be casted (i.e. converted) into each other. So for example, ASCII character 'A' is the binary equivalent of decimal integer 65 (they are both represented by 0100 0001), so casting between them (in Java) can work as follows:
System.out.println( (char) 65) prints A.
And System.out.println( (int) 'A') prints 65.
Strings
Strings are groups of characters. You can think of them as being a "string" of characters, in the same way that your mother may have a string of pearls. So they are groups of 8-bit, or 16-bit characters strung together. This grouping is more properly referred to as an array. So, properly put, Strings are arrays of characters.
Colors
For colors, it depends on the color model, but using the common RGB model, one byte is used for each of the red (R), green (G) and blue (B) values. Red would then be 1111 1111 0000 0000 0000 0000. Since this model uses three bytes per pixel (3 x 8 bits), it is referred to as 24-bit color.
(You'll note that for RGB, not only do 8-bit sets and 16-bit sets have the ability to represent way less colors, there's also a problem that 8 and 16 are not evenly divisible by 3, so 8-bit RGB color, for example is three digits for each of red and green, but only two for blue: RRR GGG BB, so red would be 111 000 00.)
Another one sentence summary:
Data is represented by binary values according to various universally agreed upon code sets, which match up particular letters/colors/sound with particular combinations of 0s and 1, and the number of things able to be represented by those sets increases exponentially with additional digits.
And if you were to draw a basic summary diagram for this assessment statement, particularly for Q1A, the following would suffice nicely:
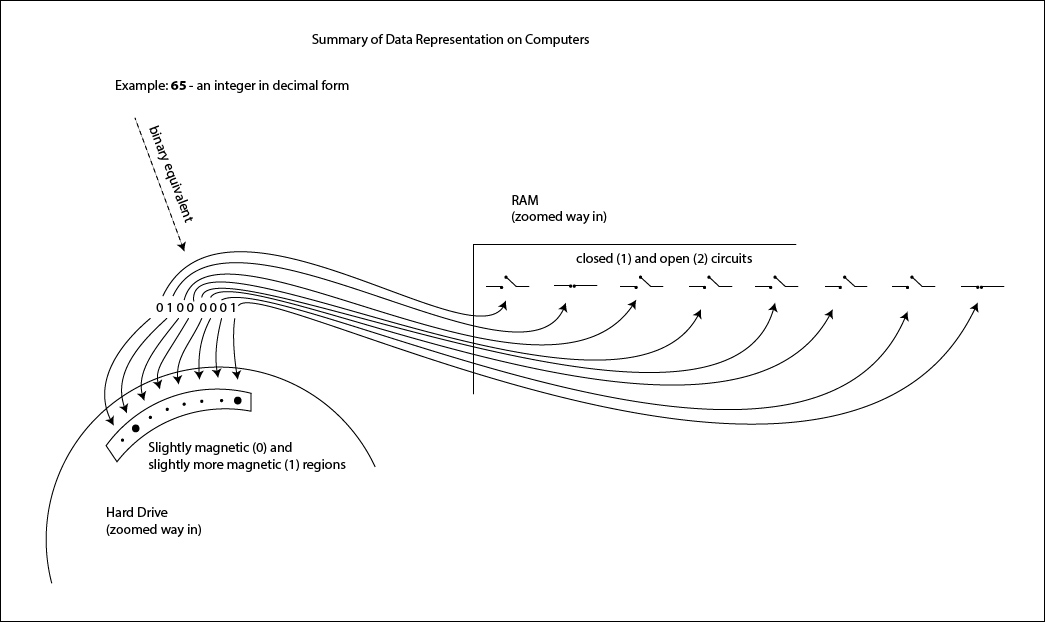
____________________________________
Q-B Hex & Colors
Q-B: Discuss "the space taken by data, for instance the relation between the hexadecimal representation of colours and the number of colours available."
First of all, as explained above, we usually work with colors combined via the RGB model (Red and Green and Blue combined), and this uses 8 bits per color, so a "24 bit color" model.
R G B
decimal green: 0 255 0
binary green: 0000 0000 1111 1111 0000 0000
hex green: 0 0 F F 0 0
decimal red: 255 0 0
binary red: 1111 1111 0000 0000 0000 0000
hex red: F F 0 0 0 0
decimal sky blue: 0 51 204
binary sky blue: 0000 0000 0011 0011 1100 1100
hex sky blue: 0 0 3 3 C C
You should be able to see that using the hex values is just easier. Green is 00FF00, Red is FF0000, Yellow is FFFF00, and Sky Blue is 0033CC, all fairly easy values to write and even to remember.
So in terms of how the number of hex digits affects the number of colors that can be represented:
Firstly, keep in mind that the number of bits used per character/number/color determines the number of things (i.e. characters/numbers/colors) which can be represented. With all data, each extra bit (binary digit) which is used to represent individual thing doubles the number of them that is available. But since computers work with groups of 8 bits usually, we tend to think of the influence of having an extra 8 bits used per characters/numbers/colors. And if you double 8 times, that's 2 ^ 8 = 256 times.
8 extra binary bits gives you 256 times more possibilities
So, for example, a 16 bit color set can represent 256 times more individual colors than 8 bit color set.
For color, we usually use hexadecimal numbering to represent RGB colors, such as FF0000 for red, and 00FF00 for green. And 2 hex digits equals 8 binary digits (FF in hexadecimal equals 1111 1111 in binary).
So for every 2 hex digits, it's also a factor increase of 256 more things that can be represented
The number of colors available in 8 or 16 or 24 bit color models is thereby 256^1, 256^2, and 256^3, which equals 256, and then 65,536, and then over 16 million. It's 24 bit color that you usually are working with on a phone or laptop, so your phone or laptop has the ability to represent over 16 million unique colors.
Here are the three most common color models:
8-bit color (i.e. two hex values color, for example F4) can represent 256 different colors.
(And by the way, if using RGB, 3 doesn't divide evenly into 8, so for the 8 bits, its: RRRGGGBB)
16-bit color (i.e. four hex values color, for example 55DD) can represent 65,536 (which is 256 x 256)
24-bit color (i.e. six hex values color, for example CC99CC) can represent 16,777,216 (which is 65,536 x 256)
RGB and CMYK models demonstrated
Hex values of various "pure" RGB colors
____________________________________
Q-C Languages & Unicode
Q-C: "Compare the number of characters needed in the Latin alphabet with those in Arabic and Asian languages to understand the need for Unicode."
Tier 1 Answer: The number of characters needed in the Latin alphabet (the one English, for example, is based on) is way smaller than those needed for Arabic and Asian languages. We only need the basic A-Z characters 0-1 numbers and common punctuation symbols to be able to store Latin characters as with the English language. Arabic and Asian languages and other world languages would need thousands and thousands of characters to be represented; think about how Chinese dialects have tens of thousands of pictograms in their language.
Remembering that computers are made to work primarily with groups of 8 bits (a byte), one group of 8 bits would be enough for Latin character languages such as English. The number of characters which could be represented by 8 bits is 2^8, or 256. ASCII, the original computer character set now uses exactly that, so it represents the most common 256 Latin characters and symbols. To go up into the thousands of available representations, it makes sense to stick with the 8 bit groupings model, and so with 16 bits, 2^16 (65, 536) different characters can be represented. And this is exactly what the standard UNICODE code set contains.
Unicode logo.jpg, Public Domain
If you had to, or chose to answer in one sentence:
The number of characters needed in the Latin alphabet which we use in English is limited, and fits well within the 256 characters permitted by ASCII, but Arabic, and Asian langauges together require much more than 256 characters, so doubling the space taken in memory to by each character to 16 bits allows 256 x 256 characters to be represented with UNICODE.
Tier 2 - Tweaked out a bit:
Latin vs. Other Languages & UNICODE
Basic ASCII (The American Standard Code for Information Interchange) initially used a 7 bit set of characters to represent letters, and in various extended ASCII sets, a full 8-bit byte is used. That means that for the basic ASCII, 2^7 characters - i.e. 128 - can be represented, and in the extended ASCII sets, 2 ^ 8, or 256 characters can be represented.
(The reason, by the way, that 7, not 8 bits were used initially is that in the original ASCII the 8th bit of the standard 8 bit byte was used for error checking during data transmission - get me to explain how the error checking worked in class sometime; there was a "check-bit".)
The Latin alphabet that we use in English has 26 lower case letters, and 26 upper case letters. So those, along with the 10 numeric digit characters (0 - 9), and 20 or so common symbols of the keyboard (!@#$%^&*( ) ;':"[]{},.< >/?\|) can all be represented within those 128 combinations of 0s and 1s of basic ASCII. Below is a picture of the first 128 characters of ASCII, which also includes various simple computer commands such as Carriage return.
But for "Arabic and Asian languages", there's not enough room in a 128 set, or even a full 256 full ASCII extended set to fit all the characters. There are tens of thousands of Chinese characters, for example.
And there you have it, in terms of the teaching note "comparing the number of characters needed..." "Arabic and Asian", and indeed a whole bunch of other kinds of languages together demand more than 256 characters to be represented. So we now have computers that work with UNICODE, which can represent thousands of characters. UNICODE uses 16 bits per character. And in so doing, computers can still work with the basic 8-bit byte. It's just that working in UNICODE, two bytes (16 bits) are read for each character. And in using 16 bits, the calculation for the number of different combinations of 0s and 1s is 2^16, or 65,536.
Try to go on-line and find a UNICODE explorer kind of website or application which allows you to view different categories and characters of UNICODE.
http://unicode.mayastudios.com/ - a good one for work with Java code
The fundamental reason why so many more characters can be represented is the same as when going from 8-bit color to 16-bit color.
With every extra bit you add, you double the number of possible combinations of 0s and 1s, and therefore the number of possible things you can represent, whether those things be colors, or in this case letters).
The math of this is: 2^numberOfBits.
2^8 = 256
2^16 = 65,536
So in extended ASCII, the 0s and 1s combinations go from
0000 0000
0000 0001
0000 0010
0000 0011
.
.
.
to
1111 1100
1111 1101
1111 1110
1111 1111
256 combinations in all.
And in UNICODE, the 0s and 1s combinations go from
0000 0000 0000 0000
0000 0000 0000 0001
0000 0000 0000 0010
0000 0000 0000 0011
.
.
.
to
1111 1111 1111 1100
1111 1111 1111 1101
1111 1111 1111 1110
1111 1111 1111 1111
65,536 combinations in all.
____________________________________
Binary a Lingua Franca?
Q-D: "Does binary represent an example of a lingua franca?"
Answer: A lingua franca is a language which most people around the world can understand. So, yes, binary, in a way does represent a lingua franca, in so far as the computers used by most people around the world are able to interpret the character codes sets ASCII and UNICODE using those 0s and 1s.
Though, this being a TOK point, how about taking it further, or rather one level up, and claim that it is UNICODE which is the lingua franca. With UNICODE, most of the people of the world can encode their visual way of communicating.
