Sample Question:

sdfsdfsf

From Sample Paper 1 - 2014:

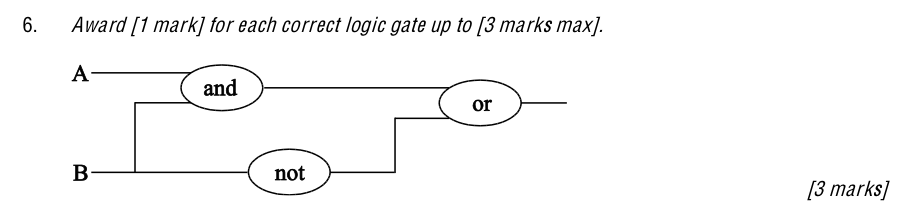
JSR Notes:

 

 

First of all a reminder of how Boolean operators function:

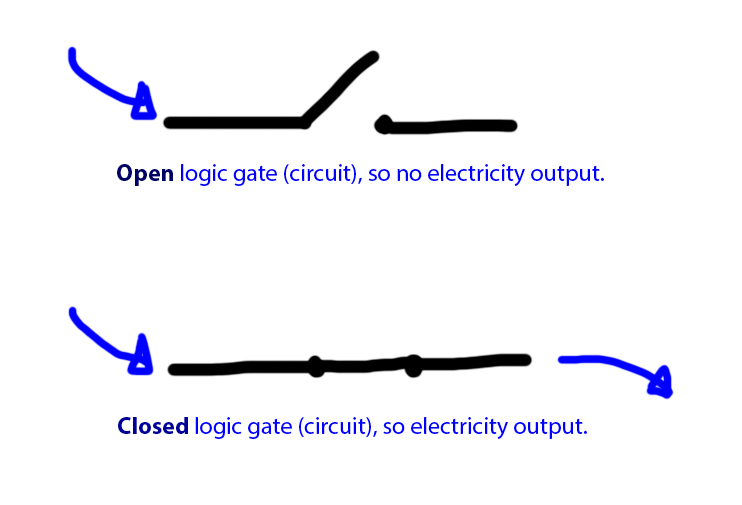
A processor contains logic gates, which are essentially circuits that can be open or closed, and so they reflect perfectly boolean logic.

"Closed" circuit = a complete circuit, electricity flows through - represented by boolean 1.
"Open" circuit = incomplete, electricity does not flow through - represented by boolean 0.

 

When there are 2 inputs to a logic gate:

For an AND logic gate the overall circuit is on (meaning it has electricity flowing through it)...

... when both input switches are closed/on.

For an OR logic gate the overall circuit is on (meaning it has electricity flowing through it)...    

... when one input switch or the other is closed/on.


For an NAND logic gate the overall circuit is on (meaning it has electricity flowing through it)...

... when not both input switches are closed/on.

 

For an NOR logic gate the overall circuit is on (meaning it has electricity flowing through it)...

... when neither input switch is closed/on (which may seem kind of weird).

For an NOT logic gate the overall circuit is on (meaning it has electricity flowing through it)... 

... when the circuit it is connected to is off. So to clarify, a NOT gate stops the flow of electricity if it was flowing before, and makes electricity flow if it wasn’t.

For an XOR logic gate the overall circuit is on (meaning it has electricity flowing through it)...

... when one switch is closed/on, but not both.

 

 

Constructing the Diagrams

Do remember that for I.B. you only need the gates written in circles, not the fancy symbols shown way below, though they are the correct ones - IN FACT IT SAYS "circle with the name of the gate" in the teaching note.

BUT MAKE SURE TO WRITE THE WORDS "NOT", "AND" ETC. FOR EACH GATE ONE WAY OR THE OTHER.

 

Here are some examples.

Note that they are all with three inputs, which is not only what IB CS requires, it is all that is required for adding two binary digits; digit A, plus digit B, plus the carry bit, (see the "Extra" note at the bottom of this page.)

 

Straight-forward:

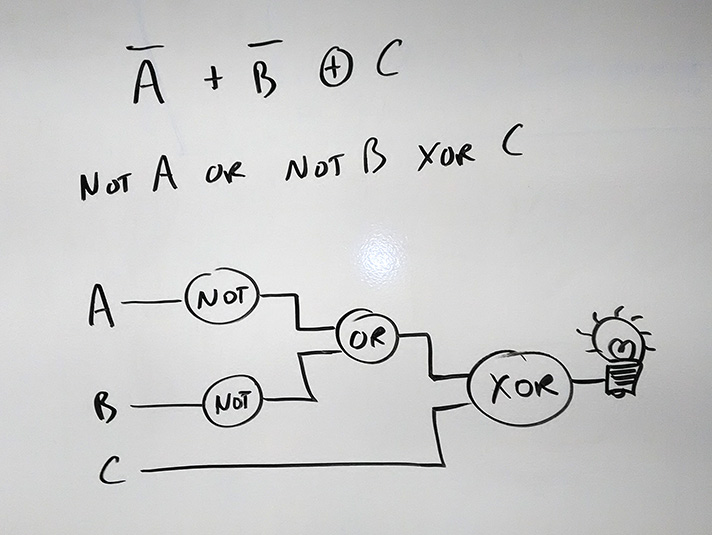
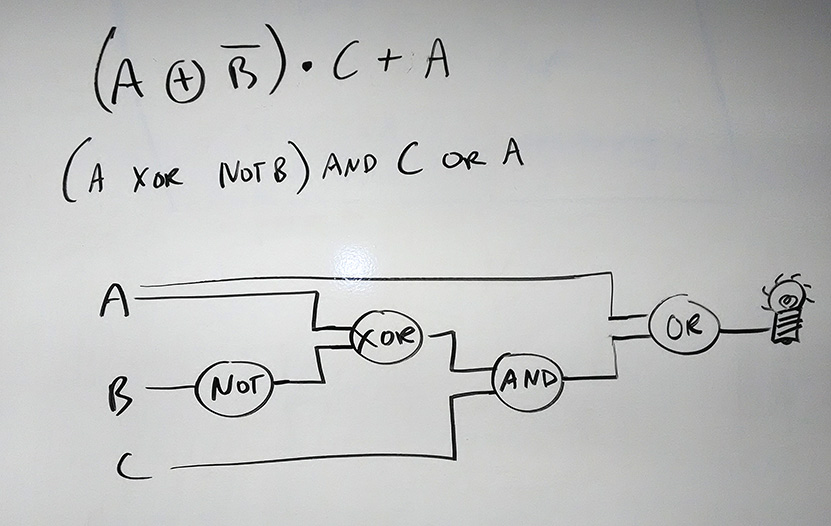
A bit more involved:

Reminder of Evaluating Compound Boolean Expressions

Recall Evaluating Arithmetic Expressions:

For example, c = a + b – (3*4) is known as an expression, and it evaluates to a single numeric value through the order of operations.
If a = 2 and b = 3, this arithmetic expression simplifies to -7:
c = 2 + 3 - (3 * 4)
c = 2 + 3 - (12)
c = 5 - 12
c = -7

Evaluating Boolean Expressions is approached the same way, step by step:

For example, ((x+y)*z == 12 && q.equals(r)) is also an expression, but a Boolean expression, so it ultimately evaluates down to a single Boolean value, in a similar fashion to evaluation of the arithmetic expression above.

If x = 2, y = 1, z = 4, and q and r are both "hello world", this boolean expression simplifies to true in four steps:

((2 + 1) * 4 == 12 && "hello world".equals("hello world"))
((3) * 4 == 12 && true)
(12 == 12 && true)
(true && true)
true

 

Here's some more practice, with answers. Note that these use the actual symbols, both for the boolean operators and the logic gates. On a test, you should just use words and circles.

Plus do some NOR and NAND examples

 

------------------- EXTRA PART 1 -----------------------

 

The Correct Symbols - you are welcome to use either the correct symbols (see below) or the circles and words (see above). I would like you to use the proper symbols, but IB only requires the words (inside circles).

If you only use simple circle gates, obviously you will put "and", "or", or "not" in the circles. But you should do that too, even if you are using the correct symbols I taught you, on the off chance that an examination marker is unfamiliar with those symbols. i.e. MAKE SURE TO PUT "AND", "OR" ETC.IN YOUR SYMBOLS.

(I'm just going to paste here the notes from the Former Curriculum, assessment statement 4.2.5, which is exactly the same as this one.)

 

 

 

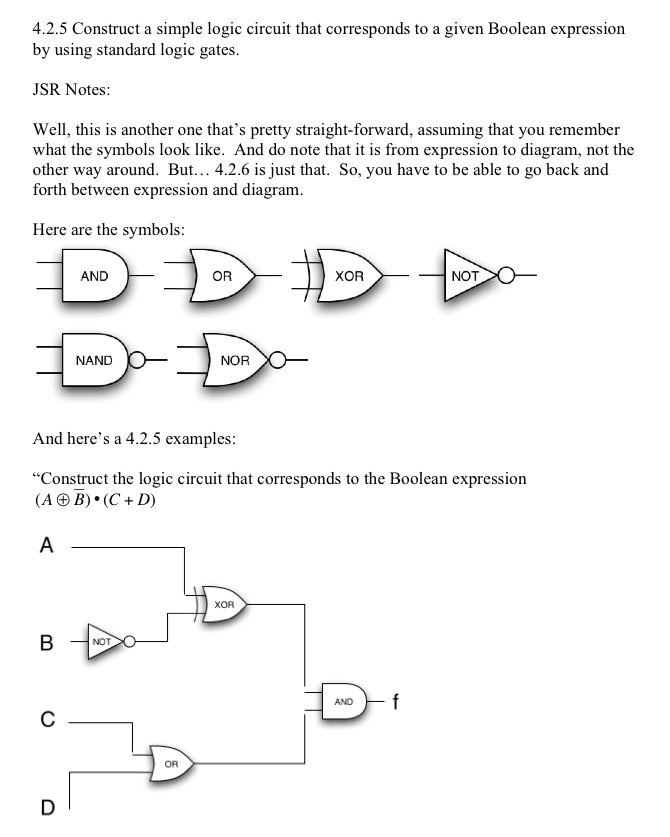
------- EXTRA PART 2: Half Adder & FORMER CURRICULUM -----------

 

Plus, you could also look at the following Former Curriculum assessment statements.

Former 4.2.5 - this one is for going the other way: from the circuit diagram to the expression.
Former 4.2.6-Extra

(And also, even these.)

(Former 4.2.2)
(Former 4.2.3)
(Former 4.2.4)

 

"La Piece do la Resistance" - Half Adder & Full Adder

Firstly, going back to the Teaching Note; it says "Problems will be limited to an output dependent on no more than three inputs." But here's the beauty, if you want to build a computer from scratch, that's all you need! Because if you can work with three inputs, that's the maximum of what is necessary to add two binary digits together! The one digit (that can be 1 or 0), the second digit (which can be 1 or 0), and the carry digit (which can be 1 or 0). Three! That's it!

And so by building circuits that account for the 8 combinations of those 0s and 1s, two binary digits can be accurately, and "blindly" added by circuitry. So just ramp that up for as many digits as you want to add, and you have a machine that can add numbers as big as you want! Then, once you have a machine that can add, it can subtract, multiply, divide, and all sorts of other things!!! (Refer back to the domino videos on 2.1.11 for an example of doing just this with dominoes.)

So here are more details and alternative explanations for this one one last wonderful key bit of knowledge. It's NOT PART OF IBCS, but it's explained well in both of the following videos.

What is it? It's how a computer does it's most fundamental operation, addition, with a fairly straight-forward combination of the logic gates we have been dealing with in the form of the half adder, and the full adder.

Enjoy!

And, thanks, Gabriel for this one: