Sample Question:

sdfsdfsf

Representing Outcomes of Two Inputs With Truth Tables

The last assessment statement was aimed at defining, as a dictionary would, AND, OR etc. logic gates. This assessment statement is about visually showing all the possible outputs of particular logic gates, depending on the inputs. We do so via "truth tables".

When there are only two possible boolean inputs, that makes for four possible variations of inputs:

A & B could be:

• off, off      (or false, false    or    0, 0)
• off, on       (or false, true,    or    0, 1)
• on, off       (or true, false     or    1, 0)
• on, on       (or true, true      or    1, 1)

 

(At this point it would be a good idea to at least take a peak at circuit diagrams to make the connection between truth tables and circuits.)

Truth Tables

We can show the results of these four possible combinations of binary input in summary form with simple "truth tables". Each boolean operator will have particular output for the four combinations of inputs/variables/digits.

The diagram below shows the AND and OR truth tables, and also their equivalent circuit representations.

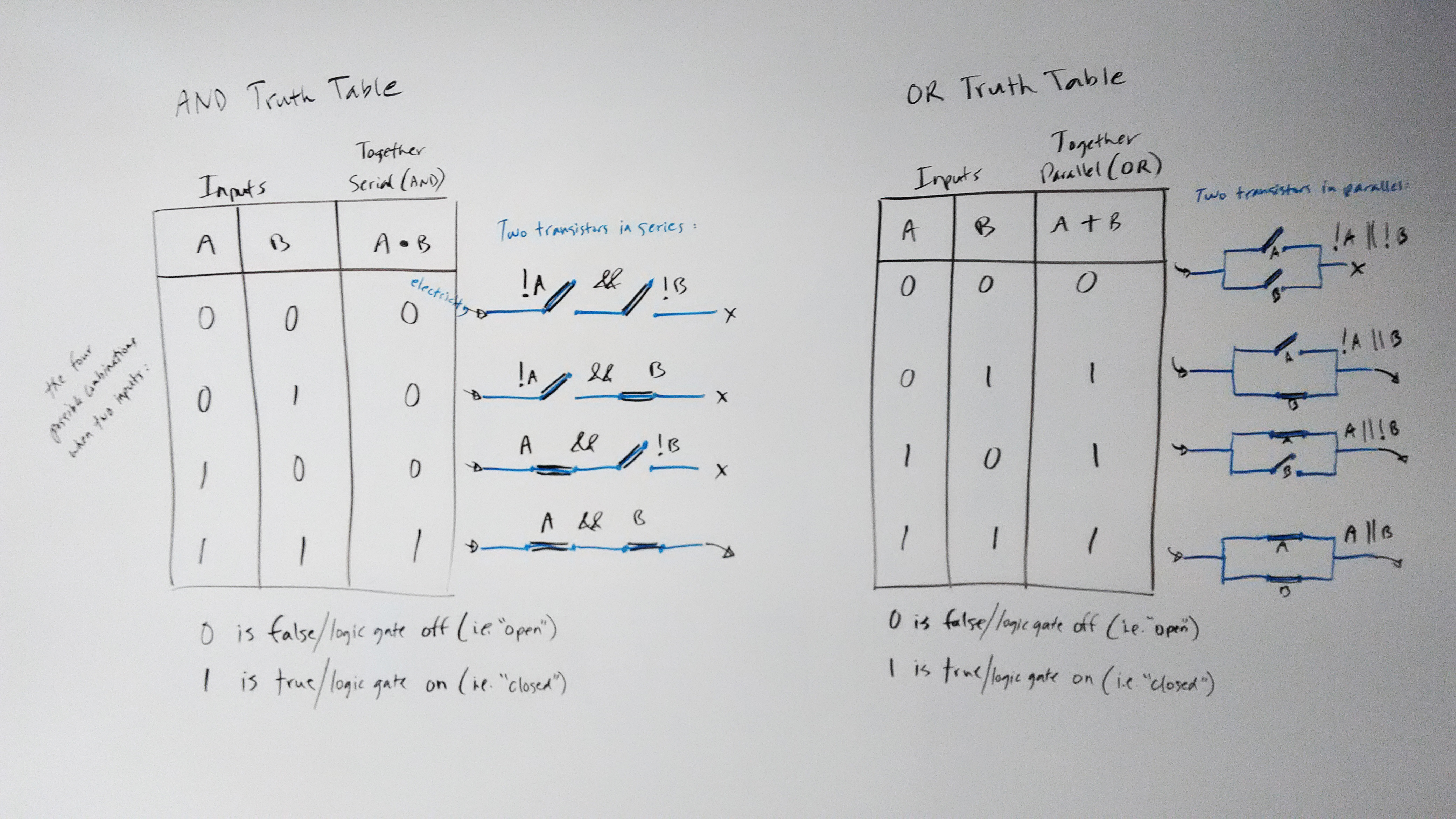
Here are the boolean operation symbols that are usually used in truth tables:

AND:   a thick dot
OR:    a + sign
NOT:   a line over top
XOR:   a + with a circle around it

Note that when doing "two step" tables like below, for example getting to NAND from AND, or NOR from OR, it's alway best to explicitly show the first step in a column of its own (rather than just do the intermediate step in your head.)

AND and NAND Truth Tables

(for NAND, think: "not both?")

OR and NOR Truth Tables

(for NOR, think "not one or the other?")
(or just think "neither?")

OR and XOR Truth Tables

(for XOR, think "one or the other, but not both?")

NOT Truth Table

 

Full Examples With THREE Inputs:

All of this, at a much deeper layer of abstraction, is about adding at a binary level. When we are adding two binary digits, often we will need to carry a digit (binary 1 + binary 1 = 0, carry the 1). So when that is the case, the next operation will need to be adding three binary digits. So When there are three possible binary/boolean inputs, that makes for eight possible result variations.

There eight possible input combinations when you have three boolean on/off switches.

A, B, and C could be:

• off, off, off       (or false, false, false,   or    0, 0, 0)
• off, off, on       (or false, false, true,    or    0, 0, 1)
• off, on, off      (or false, true, false     or    0, 1, 0)
• off, on, on       (or false, true, true      or    0, 1, 1)
• on, off, off      (or true, false, false     or    1, 0, 0)
• on, off, on       (or true, false, true      or    1, 0, 1)
• on, on, off       (or true, true, false      or    1, 1, 0)
• on, on, on       (or true, true, true       or    1, 1, 1)
  
  

We write these eight combinations for our three-input truth tables as follows:

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

And NOTE: it's not just a typical way to write them, it's THE EXPECTED WAY to write these eight combinations - zero through seven in binary. In communicating back and forth between computer scientists (or on IB CS tests!), this is the order in which you must list them, not any other way.

Here's the trick to writing down all these eight combinations correctly and quickly in the correct order.

Step 1: first write, down the page 4 zeros and 4 ones:

0
0
0
0
1
1
1
1

Step 2: then, beside the 2 zeros and 2 ones, like this:

0 0
0 0
0 1
0 1
1 0
1 0
1 1
1 1

Step 3: and then, beside those, alternating 1s and 0s, like this:

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

 

Truth Table Exercises - Three Inputs

In terms of exercises that get you to construct truth tables, you could be asked to reproduce any of the two input truth tables above, or you could be asked to construct a truth table for a particular three input situation. For example, "Construct a truth table to show the various outputs of the following circuit: a AND b OR c".

The goal is to show the outputs for each of the four, or eight possible inputs. Even without the inclusion of parentheses and NOT operators, there will be at least two steps to solve each exercise, but there may be as many as three or four steps (see examples below).

You'll NEED to keep in mind order of operations, as you go step by step through these.

Boolean Order of Operations (!!!! IMPORTANT !!!!)

• NOT takes precedence,
• Parentheses group expressions to be resolved first
• then AND, & NAND BEFORE OR, NOR & XOR
• and having taken into consideration all of the, evaluate from left to right

 

 

The goal with these is to show, via a truth table, the expected outputs based on each of the eight possible inputs.

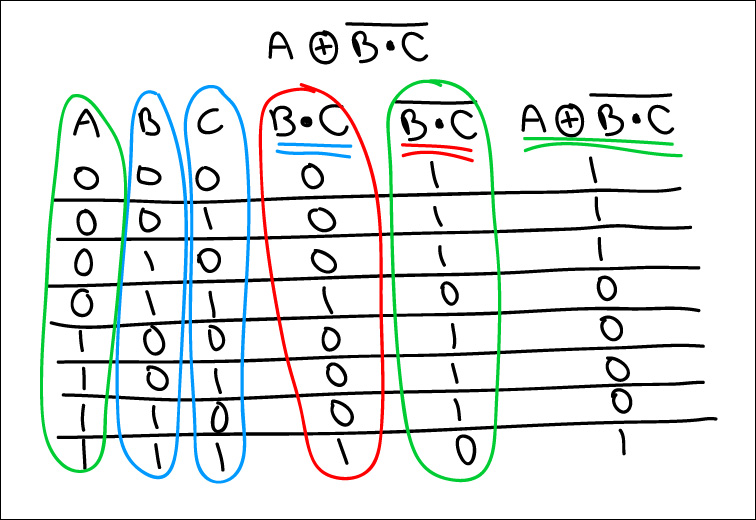
For example, below, for A and B or C, if the three inputs are all off, then the output is off, whereas if A and B are off, but C is on, there will be current coming out the other end. And so on.

A AND B OR C

 

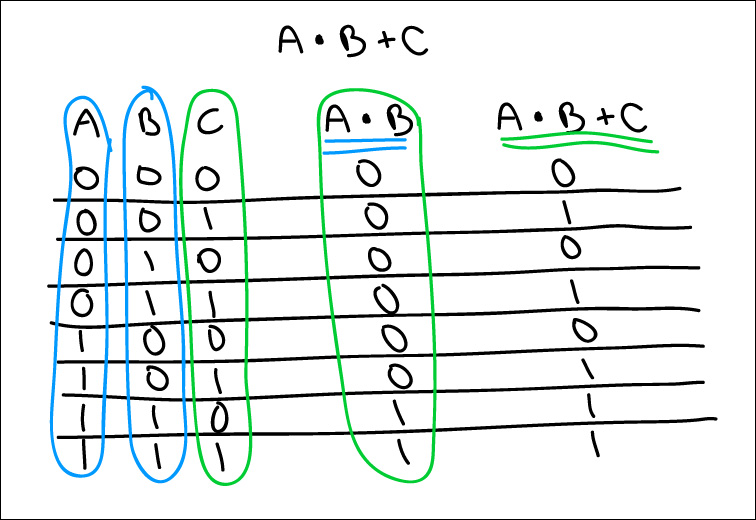
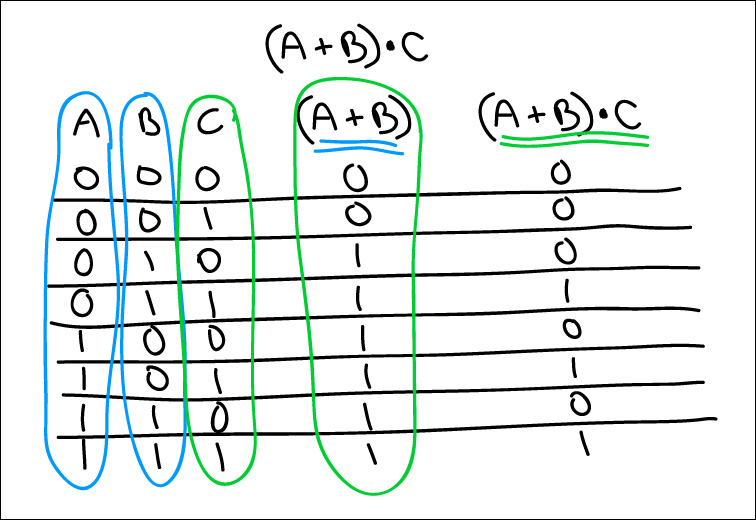
For each of these, you take them one step at a time, following the order of operations. So in the below case, you do A or B first, due to the parentheses, and then you do ***that result*** and C. That gives you your final set of results.

(A OR B) AND C

A OR B XOR C

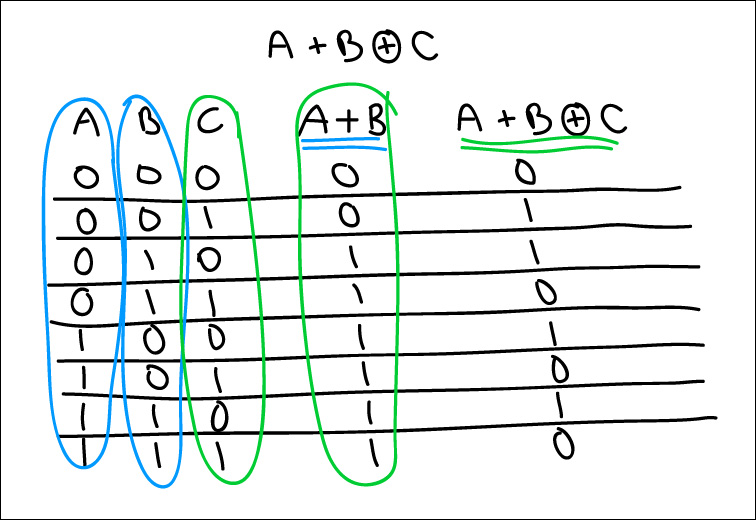
A XOR B AND C

 

 

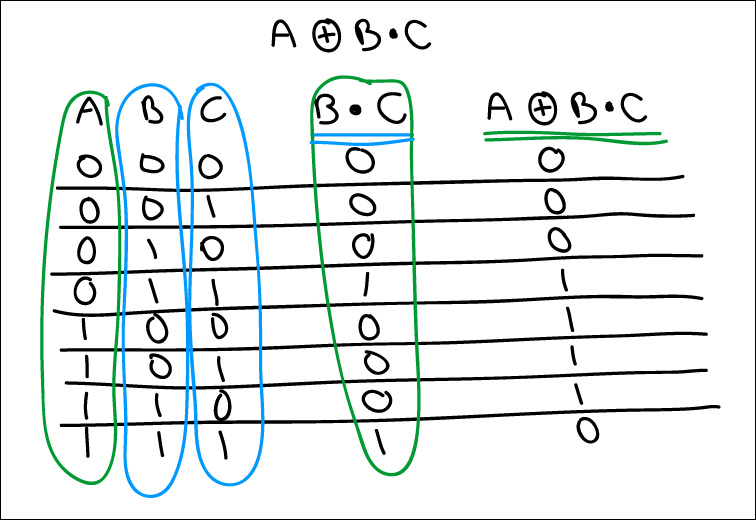
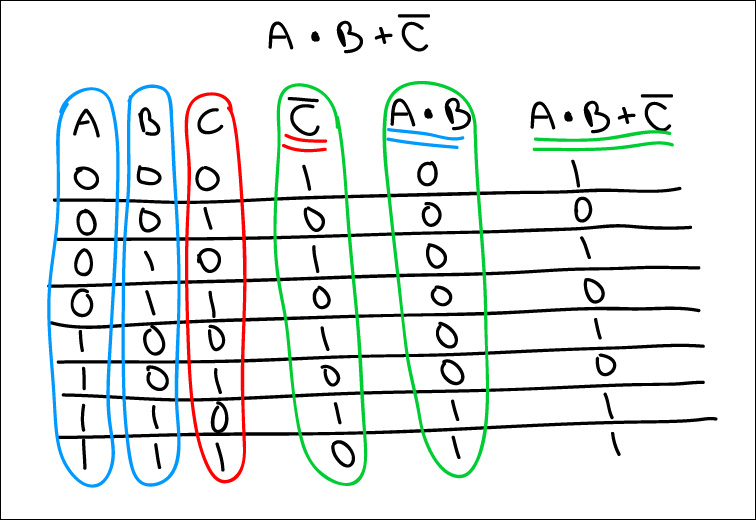
With a NOT thrown in, in the example below, it will be the first thing evaluated. Then, it's the A and B. So finally the result of A and B is combined through OR with the NOT C result.

A AND B OR NOT C

 

 

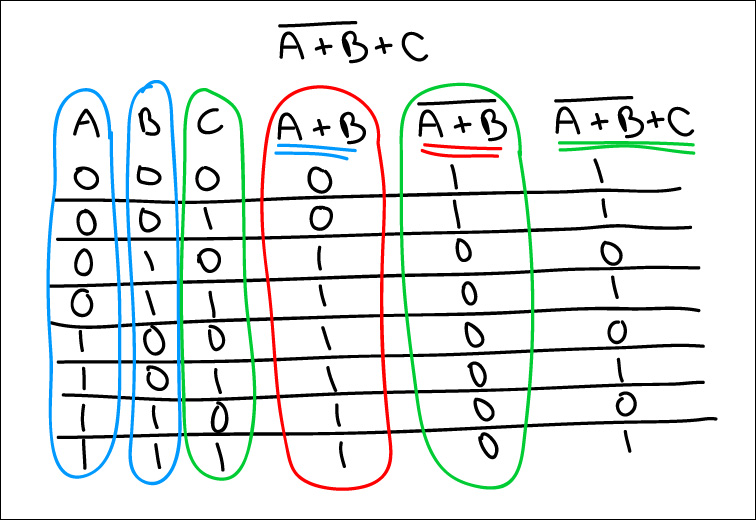
With the next example, the NOT is done first, but to know what to negate, we need to solve A OR B.

NOT (A OR B) OR C

A XOR NOT (B AND C)