--- Simple logic gates ---
2.1.11
Define the Boolean operators: AND, OR, NOT, NAND, NOR and XOR.
Teaching Note:
LINK Introduction to programming, approved notation sheet.
Sample Question (in this case, sort of...) - FORMER CURRICULUM
The method logic1(), shown below, returns the output from a particular logic gate.
The logic gate has two inputs, a and b.
//parameters a and b can only have the values of 0 or 1
public boolean logic1(int a, int b){
if(!(a==b)) return true;
else return false;
}
(a) Identify the logic gate represented by the above method. [1 mark]
(b) Construct the method logic2(), which would similarly return the output from
a NAND gate. [2 marks]
Possible "Spiraling" Through Logic Gates:
Step 1: Look at all three 2.1.11-13 in a "mercenary" way; just, how can you do these things /answer these assessment statement "at face value" And definitely mainly relate them to what you already know (possibly...): compound boolean conditions in Java.
Step 2: Then look at the advanced material, including the video on transistors, the videos showing logic gates as dominoes, and even the crazy intense Crash Course videos.
Step 3: Then, spiral through once again the more IB CS assessment statement related part, keeping in mind what you are working with is actually happening at the very low level of transistors.
And, having got to the actual transistor level, could choose to start second spiral with circuit diagrams, and work on back up to truth tables, and then general definitions.
____________________________
Preamble
The only confusing part of this assessment statement is that you can interpret/apply it four different ways. But the fundamental concept is the same.
You can "define" boolean operators by:
1. In a dictionary, Boolean Logic, or Boolean Math way.
2. How they are applied in a specific programming languages like Java.
3. A truth table. (2.1.12)
4. How they operate as actual circuit logic gates. (2.1.13)
The details will follow in this assessment statement and the next, but as an overview, and also as a very useful "second spiral" just before a test/exam, take a look at this question.
Question:
(a.) Define the AND boolean operator according to Boolean logic.
(b.) Define the AND boolean operator as it is used in compound conditions in the Java programming language.
(c.) Define the AND boolean operator by truth table.
(d.) Define the AND logic gate used in microprocessors.
Answer:
(a.) Boolean Logic AND: The overall value of an AND expression is true only when both operands are true.
(b.) Java AND operator: The AND operator in Java is &&. A compound condition using the && operator will only evaluate to true if both conditions/variables are true. For example, if boolean a = true; boolean b = false; and boolean c = true; then (a && b) evaluates to false, but (a && c) evaluates to true.
(c.) Truth table for AND:
A B A and B 0 0 0 0 1 0 1 0 0 1 1 1
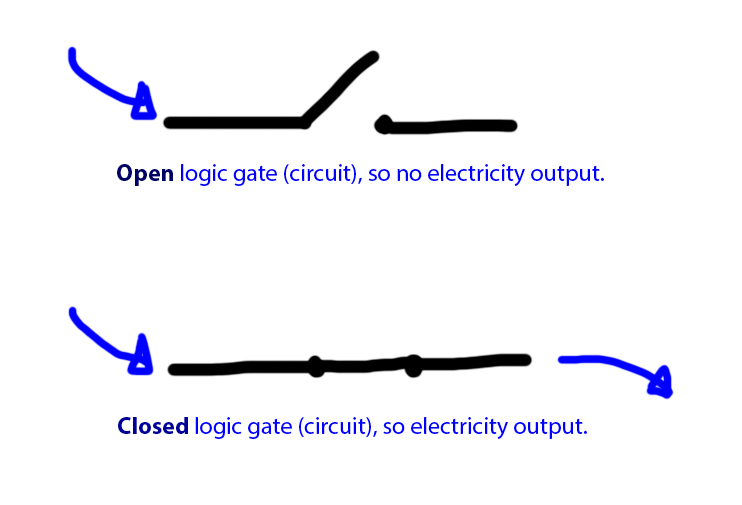
(d.) AND Logic Gate: The AND logic gate is a circuit which has two inputs. It is designed such that only when both of the circuits are closed (i.e. a closed path through which electricity can flow) will the oeverall gate allow electricity to be passed through it.
______________________________________
Boolean Operators in Programming
Of these four applications of boolean operators, it makes sense to start with Boolean operators in the context you have (likely) already seen them: programming, in particular compound conditional statements in Java.
--------> Do make a point of going to a programming IDE (like Netbeans or IntelliJ IDEA) and playing around with boolean logic again to remind yourself how it works.
Java Boolean Operators:
AND - &&
OR - ||
NOT - !
XOR - ^
NAND - !( && )
NOR - !( || )
5 package mrrayworthoctober; 6 7 /** 8 * 9 * @author John Rayworth 10 */ 11 public class ForBooleanOperators { 12 public static void main(String[] args) { 13 boolean a = false; 14 boolean b = false; 15 boolean c = false; 16 17 // AND 18 if(a && b){ 19 print "a and b are true"; 20 21 } 22 23 // OR 24 if(a || b){ 25 print "Either a or b are true (and possibly both are.)"; 26 } 27 28 // NOT 29 if(!a){ 30 print "a is the opposite of what it was first declared."; 31 } 32 33 // NAND 34 if(!(a && b){ { 35 print "It is not the case that a and be are true."; 36 } 37 38 // NOR 39 if(!(a || b)){ 40 print "It is not the case that one or the other (or both) are true"; 41 } 42 43 // XOR 44 if(a ^ b){ 45 print "Either a or b are true, but not both."; 46 } 47 } 48 49 } 50
Programs that demonstrate AND & OR and NAND & NOR
And and Or proven with Java
NAND and NOR proven with Java
____________________________
Now to the Definitions
In terms of the assessment statement, how would we define boolean operators?
Well, there are actually a couple of ways of "defining" boolean operators, one is with truth tables (see the next assessment statement), and one is the dictionary way. This assessment statement deals with the dictionary way. (But even the "dictionary" way can be either in terms of logic gates in the circuitry of computers, or in terms of boolean programming constructs - see the "Details" below.)
Here is the main focus of 2.1.11, even though all four ways of "defining" boolean operators are discussed on this notes page. Where with coding, we talk of boolean variables being true or false, and with ciruit diagrams we talk about ciruits being on or off, here we talk about boolean values being true or false.
Basic, General Boolean Operators Definitions
-----> So these are "dictionary"/math/logic basic definitions, and what this 2.1.11 is mostly geared toward. <-------
AND - the overall expression is true only if both boolean values are true.OR - the overall expression is true if at least one of the boolean values is true.
NAND - the overall expression is true as long as the two boolean values aren't both true.
(Alternatively, "returns the opposite boolean value of an AND expression").
NOR - the overall expression is true only if neither of the boolean values is true.
(Alternatively, "returns the opposite boolean value of an OR expression.")
NOT - the overall expression is true only if it is false (as weird as that sounds); i.e. it inverts the value of a boolean expression.
XOR - the overall expression is true only if only one, but not both, of the boolean values is true.
Above is the main focus of 2.1.11, even though all four ways of "defining" boolean operators are discussed on this notes page. Where with coding, we talk of boolean variables being true or false, and with ciruit diagrams we talk about ciruits being on or off, above we talk about boolean values being true or false.
More Complete Definitions; including Java example
Keep in mind that we can see that Boolean operators can actually be further defined in terms of both:
--> Boolean Compound Conditions, as in Java
--> Logic Gates, at an electrical level
| AND | Boolean Math: only when both boolean values are true is the overall expression true.
Logic gate level: Electricity flows when both input switches are closed (i.e. electricity is flowing through both of them). |
| OR |
& Logic gate level: Electricity flows when one input switch or the other is closed. |
| NAND |
& Logic gate level: Electricity flows when at most, one switch can be closed (so not both). |
| NOR |
& Logic gate level: Electricity flows though the whold circuit only when both input switches are open. |
| NOT |
& Logic gate level: Electricity flows when the input is not on (otherwise the overall gate is turned off if its input was on). |
| XOR | Boolean Math: the overall expression is true only if one but not both of the boolean values are true.
& Logic gate level: Electricity flows when one switch or the other is closed, but not both. |
-------------------------- EXTRA OPTIONAL --------------------------
Making the Connection to Logic Gates
The logic discussed above does not just function at a higher level via programming, it is fundamentally the way computers work at the most basic level, right on the CUP and other microprocessing chips.
Transistors on Microprocessors
The first thing you probably need is an idea of what a circuit, or more particularly a transistor is. And you should appreciate that in terms of a computer a transistor is the logic gate which a the single fundamental component of all microprocessing chips like the CPU. Here's an excellent introductory video:
(Backup link.)
Logic Gates
Logic gates are the basic building blocks of microprocessing chips, including the CPU and RAM memory. They are simple transistors that have one output, and usually two inputs. Current of two different levels is passed to the inputs. Depending on the kind of logic gate it is (AND, OR, XOR etc.) only certain combinations of low/high current (low-low, or high-low etc.) will cause the circuit to be closed - i.e. to allow electricity to pass through it.
Here is a diagram of an AND gate, in which both inputs have to have high current for the circuit to be closed, and electricity flow through the logic gate.
And here is a diagram of an OR gate, in which one or the other inputs have to have a high current for the circuit to be closed, and electricity flow through the logic gate.
Logic gates can be combined. Here's an example. (More on this in the next two assessment statements.)
*** A key realization for you to understand at this stage is that the result of various boolean operators and their logic gates counterparts is the same***. In fact the way a microprocessor is built from the ground results in operations entirely based on boolean logic. So everything being said about logic gates can be said about the boolean operators used in a programming language, and vice versa.
So, next, check out this great video explaining logic gates with dominoes. (Thanks Mr Walker!)
And the "logical" follow-up video. (All of this does go a bit beyond what you need for IB CS and this assessment statement, but it's kind of a shame to not go any further, because a few learnings on, and you can understand pretty well completely the basic operations of a computer.)
Plus the two appropriate Crash Course Computer Science videos (Take a deep breath!!):
Logic Gates:
The ALU:
Also note that the former curriculum "Red & Yellow" IB CS textbook has a good summary on pages 230 - 237.
Why XOR?
It is easy to understand why we may want to do something if one thing or another were true, or if both things were true, but you may wonder: why would we ever want to do something if either input was true, but not both?
The general answer is: when something else is done if both are true.
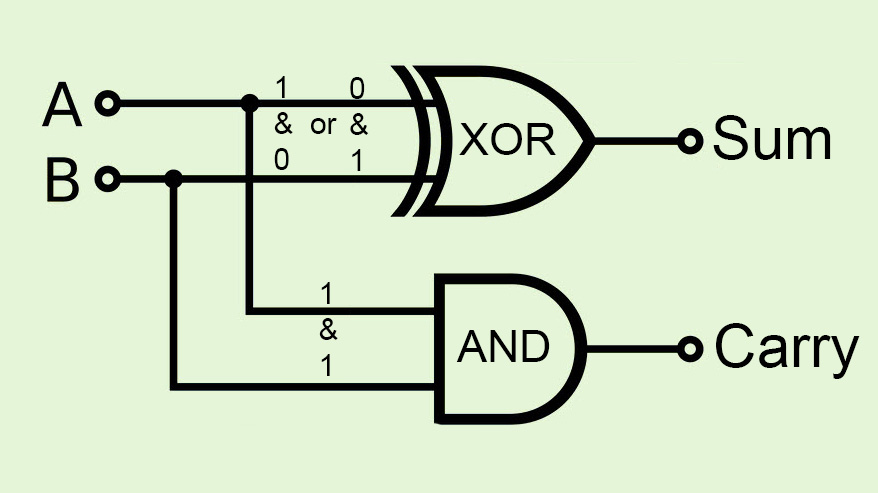
Half-adder Circuit
The best example is the most basic way that circuits achieve addition, the "half adder". With the half adder we want to add two one digit numbers, and have an extra place for the carry digit if needed. Here are the four possible input combinations A and B:
0 + 0 = 0 0 (The right hand place is the "sum" place, and the left hand place is the "carry" place.)
0 + 1 = 0 1
1 + 0 = 0 1
1 + 1 = 1 0 (In this case, we have to "carry the one".)
When one or the other input is 1, but not both the sum should be 1. A XOR B = 0 1
But when both are 1, the sum is 0, and the carry should be 1. A AND B = 1 0
After having done the next couple of assessment statements, you can look back at the following table and circuit diagram.
The truth table for the half adder looks like this:
| Sum | Carry | ||
| A | B | A XOR B | A AND B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
And so the circuit diagram for a half adder looks like this: