Computer Science:
How Computers Work & What Makes Them Faster - 2014-19 Edits
As a Pro-IT Unit - Rationale:
- Computers are a fundamental part of society. A basic understanding of how they work should be part of everyone’s general knowledge.
- An understanding of key computer components is essential for appropriate I.T. purchase and up-grade decisions.
- The same understanding facilitates maintenance and optimization of computers.
- For students considering further high school or post secondary study of I.T., basic computer science concepts will be fundamental.
As an IB Computer Science Unit - Rationale:
- What data types are, and why we have them stems from the binary nature of data storage
- Many specific assessment statements - like those relating to resources - are framed by this fundamental knowledge
Day I - Data & Code Sets
1. What kind of information do we wish computers to work with?
The primary type of data that we wish computers to work with is text/numbers. Color is the second major data category, and sound, the third. All characters, colors and sounds can be represented by codes that can be passed to computers. For example, the character ‘A’ in a Microsoft Word document could be represented by a particular code (it’s actually 0100 0001), and in the context of a photo, a certain pixel could also be represented by a particular code that a computer could somehow understand.
Pg. 113 from the classic computer text Peter Norton’s Computing Fundamentals
2. How can we communicate these things to computers?
We want to communicate these things/codes to computers, yet computers can’t hear or see or feel; but what they can do is take in, and work with electricity.
The easiest thing about electricity that a computer can recognize is whether it is flowing or not. When we type letters on the keyboard, or transmit music to our Airpods, the information is "sent" via electrical pulses that flow through wires (or in the case of wireless communication are sent though the air.) This is actually a bit of abstraction, meaning that this explanation doesn't get into all of the details how it works, but it's enough for this stage of understanding. To understand this abstraction, think of pulses analogous to if you squeeze a water hose in your back yard and release the water at certain intervals – the patterns of pulses of water released can simulate a certain code. It is the particular pattern of pulses that represents particular letters or colors or sounds.
Then, once we have loaded the words, or pictures, or sounds into our IT device, the patterns we transferred as pulses can be maintained by small electrical switches, which remain on or off in exactly the same pattern.
(Analogies – Pulses from water hose. Morse code. Patterns of lights in the lab. "Smoke signals" with the humidifier)
3. How can we represent the patterns of electrical pulses, or electrical circuits on/off?
Computer scientists symbolically represent the two different states - electricity flowing or not (and switch on or off) - with 0s and 1s. And it so happens that there exists a numbering system, which uses only the digits 0 and 1 (compared to the “decimal” numbering system that has ten digits 0, 1, 2…9). The two digit system is called the binary numbering system. Computer scientists have made sets of binary numbers, which represent the sets of things we wish to communicate to computers (characters/numbers, colors, sound pitches).
4. So what exactly do the sets of binary code look like?
The first set of code made for text-characters and numbers, which is still recognized by the majority of computers in the world today, is called ASCII. The acronym stands for the American Standard Code for Information Interchange. When we look at this extended code set, we see the 256 different combinations of 0s and 1s that can be made if you have 8 numeric places for these two digits. So the set starts with 0000 0000, then 0000 0001, then 0000 0010 ..., and goes on up to ...
1111 1110, and finally 1111 1111. The original ASCII character set actually only used seven zeros and ones to represent characters (the eighth zero or one was used for detection of errors in transmission through “parity checking.”) But anyway, each of the combinations of zeros and ones represents a character like, ‘a’, ‘H’, ‘3’, or ‘@’ (and the regular decimal digit characters 0-9 are also included.) Besides all the characters you find on a keyboard, there are other more uncommon characters such as Å and Î in the modern “extended” 8-bit versions of ASCII.
(pgs. 114, 115, 117)
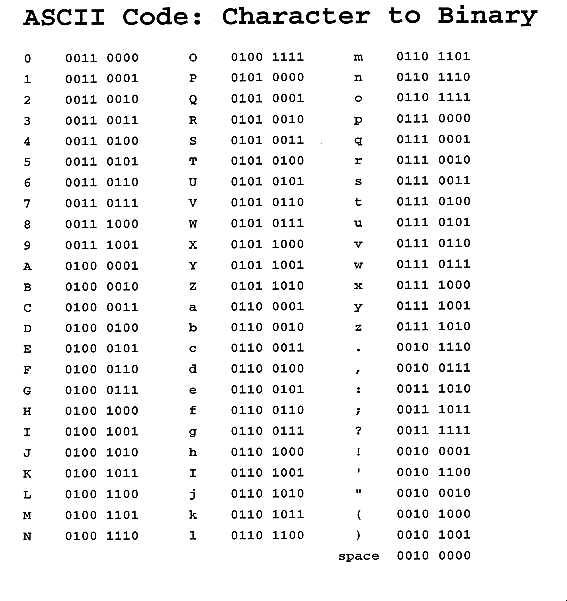
5. But aren’t there more characters in the world than just 256?
Since there are more than 256 characters that make up all the languages in the world, particularly the vast sets of Chinese, & Japanese characters, as well as other non-Western character sets, for example, Korean, Arabic and Hebrew, there is another set of code that is used called UNICODE. This character set uses all the combinations of 0s and 1s you get when you have twice as many numeric places (bits) as the ASCII set. So it starts at the binary 16 place number:
0000 0000 0000 0000, and goes all the way up to:
1111 1111 1111 1111. To get the total number of possible combinations of 0s and 1s, you take the number of digits (2) and raise it to the power of the number of places (16). This calculation of 2^16 equals around 65,000 combinations. (It’s actually 65,536.) This number is more than enough to represent all the characters the world needs to communicate to computers. (pg. 116)
6. What about representing other types of data?
Color and sound are represented by similar sets. So in an “8 bit” set for color,
0000 0000 represents black (on a computer display),
1111 1111 represents white (on a computer display),
and all the other combinations of 0s and 1s in-between represent 256 colors in total. Many Internet sites still use a standard "web-safe" 256 color set, which has existed since the time that most personal computers could only work with 8-bit color. But, as with characters, in most modern digital color situations, an 8-bit set does not offer us anywhere near enough different colors; much better is a “16-bit” set. This set goes from:
0000 0000 0000 0000 to: 1111 1111 1111 1111, representing 65,536 different colors in total. (That’s about the same number as the seating capacity of a large football stadium.) In fact, if this isn’t enough to satisfy a certain color (or sound) related task, computers can recognize millions of colors or sounds by using 24 numeric places for each color/sound. This makes the calculation for the total number of combinations of 0s and 1s to be 2^24, which is in the millions. (It’s actually 16,777,216.) That’s plenty of different colors (or sounds) to get to choose from!
(Demo: Remote Desktop screen sharing of thousands, rather than millions; or go into the Photoshop color picker to see the difference.)
(Quirky Instructional Idea:
Think about uploading the world's smallest picture - a picture that is one pixel only.
If you used 8-bit color: ----------> 0000 0000 --------> there would be 256 possible choices of color for the one-pixel picture.
Using 16-bit color: ----------> 0000 0000 0000 0000 --------> 65,536 possible choices of color for the one-pixel picture.
Using 24-bit color: ----------> 0000 0000 0000 0000 0000 0000 --------> 16,777,216 possible choices of color for the one-pixel picture.)