5.1.2
Identify recursive thinking in a specified problem solution.
Teaching Note:
LINK Binary trees.
Sample Question:
sdfsdfsf
JSR Notes:
So here, you would be given a real-life or programming situation, and be asked to spot the recursive solution - which, at one level is pretty easy; just look for another instance of a particular method being called within one of the same name.
Example 1: As your first example, look back to 5.1.1 and the Little Old Lady code.
Example 2: And the following of recursion in Flash, with a scripting language you are probably not familiar with. But you can, simply, identify it as recursion, because there are calls to the testNeibhbor() method within the testNeighbor() method.
Flash Game Recursion Example
Here's the game. (In 2020 Chrome still plays Flash files if you allow it.)
Here's the code:
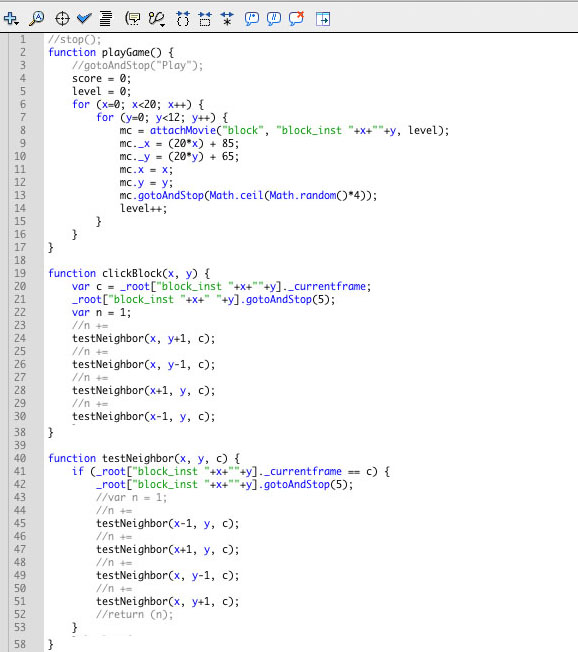
Example 3: The recursive binary search (explanation to follow in D.4.2 - this is just here so you can "identify" it is recursive.
public static int recursiveBinarySearch(int[] arr, int low, int high, int key) {
if (low < high) {
int mid = low + high/ 2;
if (key < arr[mid]) {
return recursiveBinarySearch(arr, low, mid-1, key); //<-- Ah ha!! Recursion!
} else if (key > arr[mid]) {
return recursiveBinarySearch(arr, mid+1, high , key); //<-- Ah ha!! Recursion!
} else {
return mid;
}
}
return -1;
}
Example 4: Factorial!
public int factorial(int n) {
if(n == 1){
return 1;
}
else{
return n * factorial(n - 1); //<--- Ah ha!! Recursion!
}
}
Example 5: Traversing a binary search tree (explanation to follow in D.4.2 - this is also just here so you can "identify" it is recursive.
private String inOrderString = "";
private String traverseInOrder(StudentNode, String 2){
if(p != null){
traverseInOrder(p.getLeft(), inOrderString); //<--- Ah ha!! Recursion!
inOrderString += p.getValue().getName();
traverseInOrder(p.getRight(), inOrderString); //<--- Ah ha!! Recursion!
}
return inOrderString;
}
So, we do need to go beyond simple identification here... but this is continued on D.4.2