HL extension (45 hours)
Topic 5— Abstract data structures (23 hours)
5.1 Abstract data structures (23 hours)
This will be examined at the level of diagrams and pseudocode.
Students should be able to describe the most common data structures (arrays, stacks, queues, linked lists, binary trees) and the most common data processing operations on each of the basic data structures (addition, deletion and retrieval of data, traversal, searching for a given data, sorting of data into some order).
This should be taught and connected to flow charts, pseudocode and programming in the SL/HL core.
The basic ideas and their application should be illustrated with non-computer examples. Each basic idea should then be practiced in specific algorithmic contexts using concepts drawn from flow charts, pseudocode and programming.
--- Thinking recursively ---
Identify a situation that requires the use of recursive thinking.
Teaching Note:
Suggested practical activity: snowflakes and fractals, towers of Hanoi.
Sample Question:
sdfsdfsf
JSR Notes:
************ If not doing in combination with the OOP extension, maybe 5.1.1 - 5.1.3 for the OOP extension, where recursion is repeated. *** if only because stacking has not been introduced at this point in the curriculum.
Recursion both here and in OOP Extension
First of all note that 5.1.1, 5.1.2, and 5.1.3 are the Topic 5 assessment statements for recursion. But in the Option that we are doing, which is Object Oriented Programming (OOP), D.4.1, D.4.2, D.4.3, and D.4.4 are also recursion and mainly ask the same thing. (From before: So I am putting ***everything*** here in 5.1.1 - 5.1.3; it make no sense to repeat it, nor to split the coverage. So just make sure that in preparation for the Paper 2, for you, the OOP paper, you come back here, as the links direct you... nope; they are now together.)
What situations require Recursion?
First of all note, as it is put in D.4.2:
Students should understand that recursion can be applied to a small subset of programming problems to produce elegant solutions. Students should also understand that recursive algorithms are rarely used in practice.
But, here are three situations where we can usefully apply recursion:
1. The recursive solution mirrors real life
In real life there are sometimes problems that are solved by solving a similar problem with a different set of values, and that problem, in turn, is solved by solving a similar problem with still different values, and so on,and so on, until an overall resolution is found. These are actual recursive situations, which therefore can, and should, have recursive solutions coded for them.
2. Recursive solutions are often more "elegant"
Recursive solutions often will be more elegant than their "iterative" counterparts, in that they take up a lot less lines of code. By choosing such a shorter, more elegant recursive solution, it often will be easier to read and follow. Though keep in mind that the reason this is possible goes back to reason 1; it mirrors the real life situation.
3. No iterative solution is possible
This is the case where you actually require recursion. Often times with such recursive solutions, there actually is no iterative solution. So that is the definitive reason to use a recursive solution: there is no other way to do so.
Recursion Analogies
(Refer also to "Stacking Analogies".)Recursion Analogy 1 - "George"
You ask me who took the nice picture, and I say "George". But you don't know who George is, so you ask me a question:
"Who_is (George)?"
I answer, "He's Alexander's brother".
But with this information, you still don't know who George is because you don't know who Alexander is. So you have to break down the problem further ("divide and conquer principle"), and ask another instance of the same sort of question ("self-same principle").
"Yeah, but who_is (Alexander)?"
I answer, "He's Elizabeth's father."
Hmmm... still no satisfaction...
"Sure, but who_is (Elizabeth)?"
I answer, "Oh, that's actually Liz's real name."
You still don't know how to put who the picture taker is in context, but you sure hope you're getting closer...
"Well, who_is (Liz)?"
I answer, "Liz is Billy Smith's mother.""Ah ha!, I know Billy Smith". This is what we call the "base case"; meaning the case where, having drilled down several levels, there is finally "an answer", and no more recursive calls are required.
So now you can work your way back down through the stack:
Billy Smith's mother,
who is named Liz,
who is also named Elizabeth,
has a father whose name is Alexander,
who has a brother named George.
That's who George is:George is Billy Smith's mother's father's brother; i.e. Billy Smith's great uncle.
The recursive method is asking who_is a certain person, but each time you call the method you are sending a different argument. And fortunately there is a base case which is a person that you know, so all the questions are answered (in LIFO fashion), all the methods thus completed.
Recursion Analogy 2 - "Antananarivo"
Wow, you're a really good programmer. At some point I'd like to come over and do some recursive programming with you. So tell me, where do you live?
So, where_is(your house)?
On Rue Andriantsihoarana? (This doesn't help, so have to put that where_is on a stack of undone where_is methods and call another where_is method)
Ok, where_is(Rue_Andriantsihoarana)
It's in Analamahitsy. (ditto)
Sure, but where_is(Analamahitsy)?
It's in Antananarivo. (ditto)
Fine. That rings a bell... where_is(Antananarivo)?
It's the capital city of Madagascar. (ditto)
Madagascar... heard of the movie, but where_is(Madagascar)?
It's the big island country off the east coast of Africa.
- and this is an answer that actually tells us something that makes sense to us, so it's the base case from which we can then work up through the stack of unanswered questions:
A ha! So now if I go to Madagascar,
and then to Antananarivo,
and then to Analamahitsy,
and then to Rue Rainizanabololona,
I will find you!
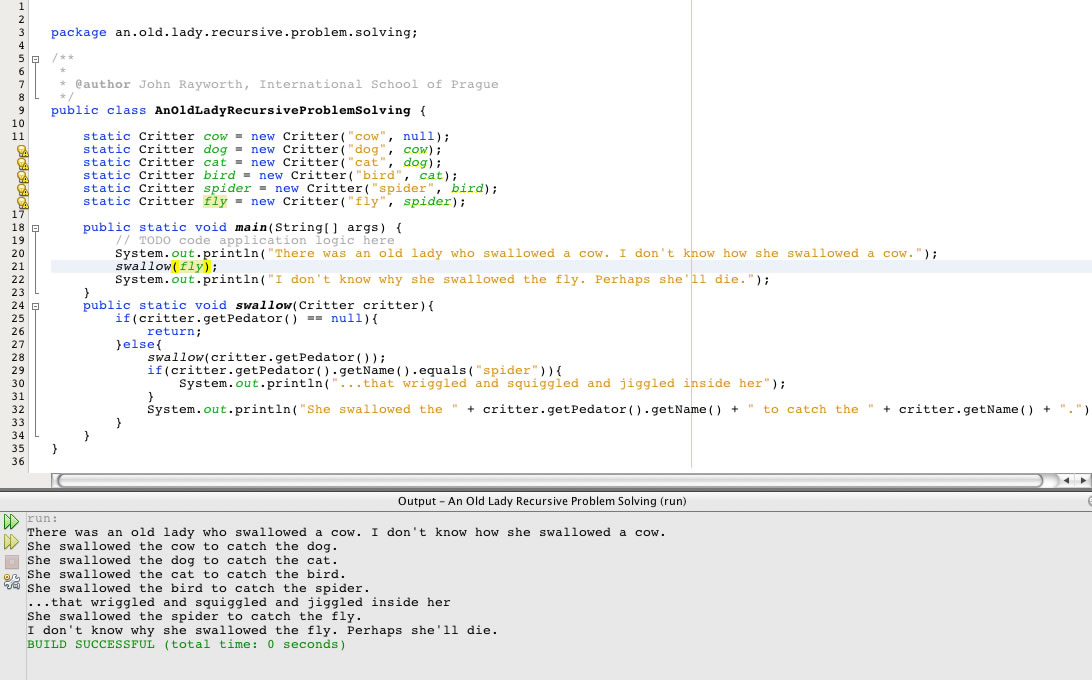
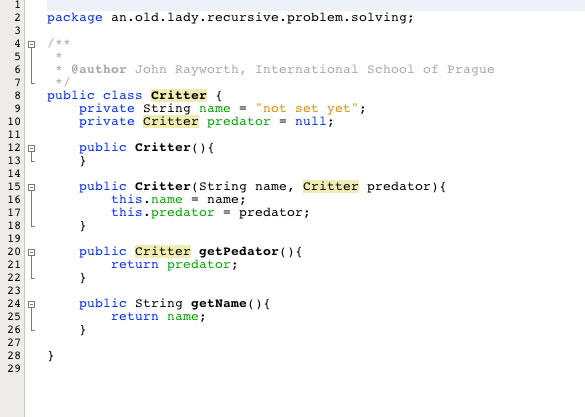
Recursion Analogy 3 - "The Little Old Lady"
How come that little old lady over there swallowed a cow?
So, why_did_she_swallow_the(cow)?
She swallowed the cow to eat the dog.
Yeah, but why_did_she_swallow_the(dog)?
She swallowed the dog to eat the cat.
Sure, but why_did_she_swallow_the(cat)?
She swallowed the cat to eat the bird.
Ok, but why_did_she_swallow_the(bird)?
She swallowed the bird to eat the spider.
Fine, but why_did_she_swallow_the(spider)?
She swallowed the spider to eat the fly.
Ok, but why_did_she_swallow_the(fly)?
Because it's just one of those things; sometimes a little old lady has a fly fly into her mouth by accident,
and she swallows it. (The base case answer.)
A ha! So the reason she swallowed a cow was that a fly flew, inadvertently, into her mouth,
and so she swallowed a spider to catch the fly,
and she swallowed the bird to catch the spider,
and she swallowed the cat to catch the bird,
and she swallowed the dog to catch the cat,
and she swallowed the cow to catch the dog. Gotcha!
Old Lady Recursive Problem-Solving
The question is: whyDidSheSwallow(TheCow);
Fast foward to 5:48 for the finale! And the answer...
With the Little Old Lady nursery rhyme, each time through we ask a question and can only answer it by asking further, similar questions. The nursery rhyme actually ends up with the cute, but non-recursive, "she swallowed a horse, she's dead of course." But on up to this, culminating with the cow, each question is answered recursively with other similar questions, down to the base case of her having swallowed a fly. Indeed the only way to get to the bottom of this case is to keep on asking the "why did she swallow a..." question, until there is a reasonable answer (noting that little old ladies do indeed, at times, swallow flys which inadvertently buzz into their mouths).
And note that for the print out to work, the position of the println( ) will have to be moved within the swallow( ) method.
Other Teaching Note Examples
Check out these YouTube examples of snowflakes and fractals, towers of Hanoi.
Snowflakes:
Fractals:
Entire screen game: http://entire.spacebar.org/
"You can't win the game. It only exists to destroy your mind." And I think due to its recursive nature it will destroy your computer too... or at least slow it down a whole lot. So be careful!
Towers of Hanoi:
With the Towers of Hanoi problem, you have to move all of the disks from one pole to another, using a third; the only thing is you cannot ever put a larger disc on a smaller one. See below for the Java recursive solution. You can do an iterative solution, but it's four times as long, and harder to read and follow.
public class TowersOfHanoi {
public void solve(int n, String start, String auxiliary, String end) {
if (n == 1) {
System.out.println(start + " -> " + end);
} else {
solve(n - 1, start, end, auxiliary);
System.out.println(start + " -> " + end);
solve(n - 1, auxiliary, start, end);
}
}
public static void main(String[] args) {
TowersOfHanoi towersOfHanoi = new TowersOfHanoi();
System.out.print("Enter number of discs: ");
Scanner scanner = new Scanner(System.in);
int discs = scanner.nextInt();
towersOfHanoi.solve(discs, "A", "B", "C");
}
}
Plus a couple of other brain twisters. Thanks Ta!


And one more interesting application of recursion to adjust lighting in a game at java-gaming.org.
JSR: Plus
646 recursive stacking in memory (jpg1) (jpg2) (poor board diagrams that need re-doing)