Sample Question:

sdfsdfsf

JSR Notes:

This is a copy and paste of what is found in Topic 5.1.6 (stacks), 5.1.8 (queue). More details were given above in the OOP Topic. So in case you're thinking that much or all of this is a review, you're right!

For these, I have used this assessment statement's three "should be able to"s from the Teaching Notes to structure this introduction, so: descriptions, diagrams, and applications.

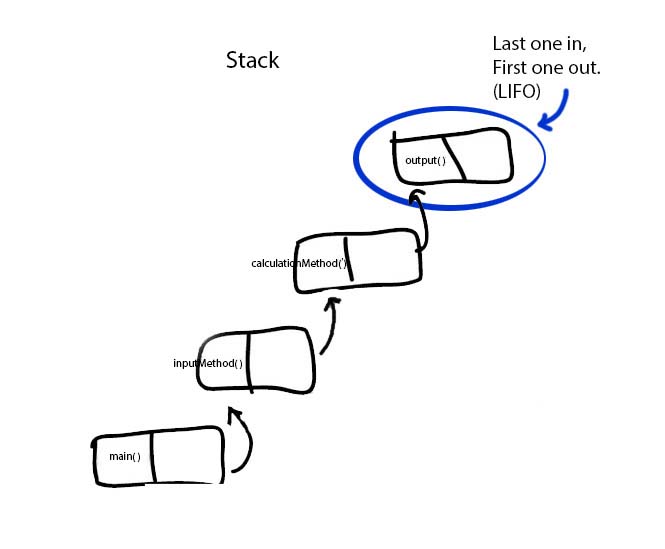
Features of the Stack ADT:

Description/Characteristics

- Stacks are particular implementation of lists, which operate in a LIFO manner.

- Since they are lists, stacks are made of a "chain" of self-referencing nodes; i.e. nodes of the same type that point to each other.

- Items can be added, or "pushed" onto one end of the stack (most conveniently, the head).

- Items can be taken from, or "popped" from the same end of the stack, and so operating in a LIFO basis (Last In, Last Out).

- It is important that checks can be made to see if the stack is empty, thus preventing the error of trying to access something that is not there.

Diagrams

(This diagram actually shows pushing and popping to/from the tail. This is easier in one way to conceptualize, but is inefficient compared to working with the head.)

Applications

General:

- Any process in which the last one on the stack should be the first one that is next dealt with, and so taken off the stack.

Analogies:

- A conventional analogy is when plates are stacked on top of each other in a cafeteria; it is impossible to take from the bottom of the stack, and so we always take the top plate off of the stack.

- In fact stacking of physical objects, like magazines on the coffee table of the living room.

Computing:

- 1. Errors which can interrupt other events, including other errors, cause stacking of those other errors and other events. This is the case because if anything, including an error itself, is interrupted by a new error, it's that last error that has to be handled first, before the other ones can be.

- 2. Method calls in the middle of other methods cause stacking of the unfinished methods. In this case the unfinished method that has made the call goes on a stack, and waits for the called method to be finished. This can go many levels deep; for example, main( ) calls method1( ), and method1( ) calls method2( ), and method2( ) calls println( ). When println( ) is being executed, all of the method calls before it are on a LIFO stack waiting to be finished.

- 3. Recursion. Recursion is a process in which a method is interrupted by calls to other instances of itself. This accomplishes repetition without the use of a conventional structure such as a for or while loop. Since functions get interrupted, they are not finished, and so they have to be put some place, on a "stack", where they wait to be handled. Once the other method that they themselves called get finished, they can then also finish.

 

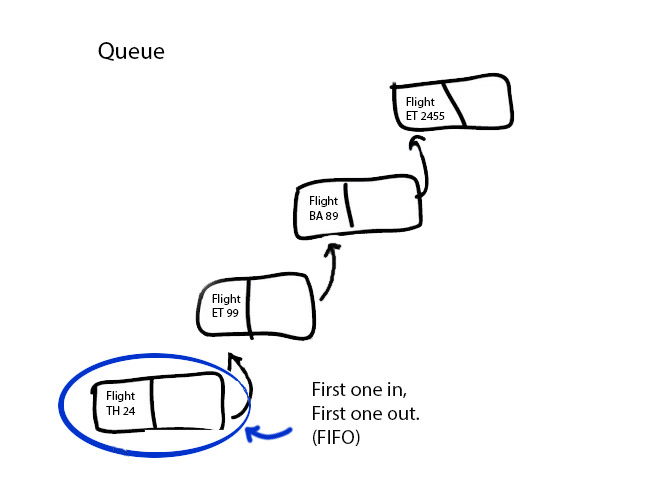
Features of the Queue ADT:

Description/Characteristics

- Queues are a particular implementation of lists that operate in a FIFO manner (first-come-first-serve).

- Since they are lists, queues are made of a "chain" of self-referencing nodes; i.e. nodes of the same type that point to each other.

- Items can be added, or "enqueued" onto the head or tail of the queue.

- Items can be taken from, or "dequeued" from the opposite end that they were enqueued to. That way the items that have been there the longest get priority of access, and so queues operate in a FIFO basis (First In, First Out).

- It is important that checks can be made to see if the queue is empty, thus preventing the error of trying to access something that is not there.

Diagrams

 

Applications

General:

- Queues function in much the same way that lines or queues function in most of the civilized world, in that the first one in the line is the first one served; there's no butting into the line.

Analogies:

- Other than queues of people lining up for food, or tickets at a movie theatre, a good common example is airplanes queuing up to take off from an airport. The first one to taxi out to the runway is the first allowed to take off. Once that plane takes off, the next one in line is the one that takes off. New planes line up at the back of the list/queue.

Computing:

- 1. In terms of the functioning of a computer, queues will be used whenever tasks are non-urgent, and at the same level of priority as the other tasks waiting for the CPU to execute them. (A Topic 6 example is CPU polling.)

- 2. And in terms of programs we will make, whenever we have a list of things to do or deal with, and they also are all of equivalent importance and priority, a queue is the most equitable way to deal with them one by one.

- 3. A print queue or a queue for any other network service such as this. It only makes sense that the print jobs etc. are fairly handled in a first come-first serve basis.

- 4. Computer modeling of physical queues (eg. supermarket checkouts). Taking the example mentioned above in the Teaching Note, a simulation to test efficiencies of various arrangements of supermarket checkouts would have to function the way that they do in reality, which is the first one in line is always the next person dealt with.

- Note that a queue can function in a linear way, or a circular way as well:

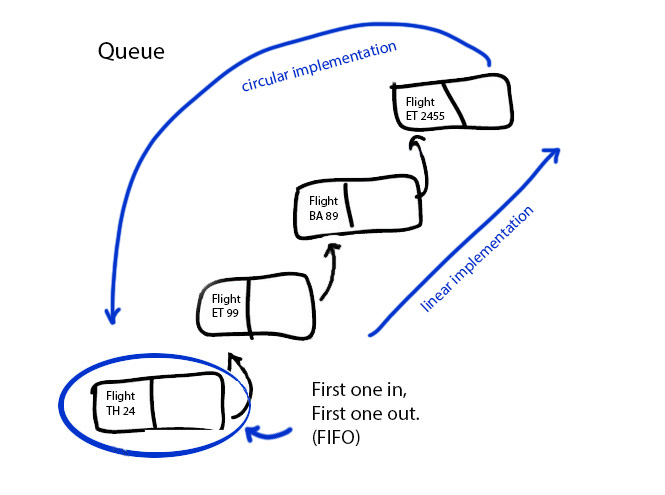
Features of Binary Tree ADT:

(Refer to 5.1.14 also, for more implementation details.)

Description/Characteristics

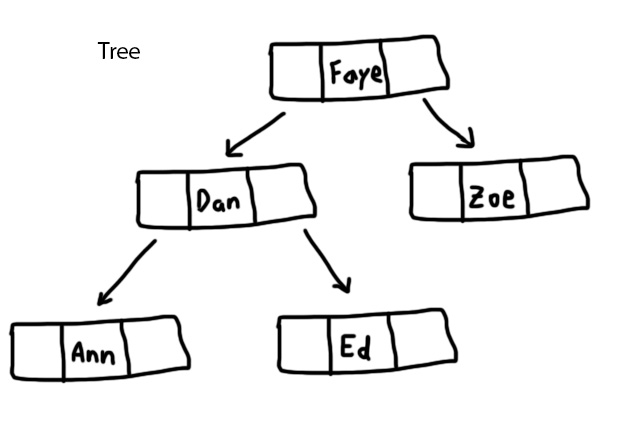
- Binary trees are a data structure that is also properly referred to as binary search trees. They are ideal for storing data that has to be searched efficiently regularly.

- A binary tree is made of nodes which have two pointers each: one pointer pointing to the right, to all of the nodes which contain items "greater" than itself, and one pointing to the left, to all of the nodes "lesser" than it.

- The tree starts assembling itself with a "root" node (which, to have a balanced tree, should be a "middle" value of the set).

- Items are added by progressing down through the tree, asking at each node whether they are "greater than" or "lesser than" the current node, and then being attached when they get to the "end of the line".

- Because of the way values are added, they are naturally sorted.

- Searching can be done in a binary way, because of this natural sorting process, since at every step through the binary tree when searching, half of the remaining nodes are eliminated from the search.

- Through various algorithms, nodes may be effectively deleted from the tree by re-linking nodes around them.

Diagrams

Applications

- The binary search tree is the "be-all-and-end-all" of data structures, in that it is the best of both worlds, with regard to both memory management and searchability. It is dynamic in nature, allowing items to be added and deleted without memory penalty, but it is also binarily searchable.

- So whenever a data structure has an unknown and/or changeable size, and it also will be frequently searched, the binary search tree is an ideal choice.

- Or put another way (the Teaching Note way) a binary tree can be used to efficiently store and retrieve unique keys.

- Examples include all sorts of data that needs to be managed and searched, yet whose number of items grows and/or shrinks. So to take just one example, the student database of a school with big numbers, and fluctuating enrollment with students arriving and leaving regularly, so like is the situation at a big international school.

 

***Note that since binary trees appear in the OOP topic, and so do reference mechanisms, even though they were gone over in a lot more detail in Topic 5, they are fare game here too, as seen, for example on the May 2017 paper 2.