Sample Question:

sdfsdfsf

JSR Notes:

List ADT F.: Tracing usage of ArrayList & Linked List

This assessment statement states algorithms described in D.4.9 - D.4.11, so it's not just LinkedList from the last assessment statement, it's a static implementation of lists, the List ADT, and both ArrayList and LinkedList. For making algorithms (as in D.4.10), yes, it's just with the methods listed. But in this case, for tracing, it's not just tracing programs with that subset of methods, it's all of them. Though, as the Teaching Note suggests, definitions of the methods used will be given.

See the sample paper pages 43-46 (below) for sure, along with former papers to get practice with any kind of tracing.

From past paper printouts that can't leave the class, look up the following questions.
(JSR Note: The digital version of these is in a folder "Past Papers LOOK INSIDE".)

As with all past papers, it is best to prioritize the latest exams. So working backward:

Nov. 2017: Q 18 - page 18
May 2017: Q 15 - page 16
Nov. 2016: Q 20 - page 15
May 2016: Q 17 (a) and (b) - page 17 - but not really; more arrays only
Nov. 2015: Q 18 - page 18
May 2015: Q 18 (c) and (d) - page 16 Most of these others are construction questions primarily.
Nov. 2014: Q 17 - page 18
May 2014: Q 17, - page 19

Since there are very few tracing questions from past papers, the best thing to do would be to look at the Marking Schemes of the above questions.

Practice questions .rtfd compressed file.

 

Tracing Examples

Though, as noted above, tracing can be any of the ADTs mentioned in the previous three assessment statements, the most likely is still LinkedList, so here are three examples.

Q1. What is the output after the following code is run?
The output of the following code is done for you by way of comments to the side.
 1 
 2 import java.util.LinkedList;
 3 
 4 public class UsingLinkedList {
 5     public static void main(String[] args) {
 6         stackOfStrings();
 7     }
 8     public static void stackOfStrings(){
 9         LinkedList<String> namesList = new LinkedList<String>();
10         namesList.addFirst("Joe");                   //Joe
11         namesList.addFirst("Betty");                 //Betty Joe
12         namesList.addFirst("Phil");                  //Phil Betty Joe
13         System.out.println(namesList.removeFirst());  //Betty Joe         //Phil output
14         System.out.println(namesList.getFirst());     //Betty Joe         //Betty output
15         namesList.removeFirst();                     //Joe
16         namesList.addFirst("Sue");                   //Sue Joe
17         namesList.addFirst("Charles");               //Charles Sue Joe
18         namesList.removeFirst();                     //Sue Joe
19         namesList.addFirst("Chisanga");              //Chisanga Sue Joe
20         System.out.println(namesList.removeFirst());  //Sue Joe            //Chisanga output
21     }
22 }


Q2. What is the output after the following code is run?

 1 import java.util.LinkedList;
 2 
 3 public class MoreLinkedListQs {
 4     public static void main(String[] args) {
 5         LinkedList<Integer> numbers = new LinkedList<Integer>();
 6         numbers.addLast(99);
 7         numbers.addLast(888);
 8         numbers.addLast(11);
 9         System.out.println(numbers.element());
10         numbers.addLast(22);
11         numbers.addLast(33);
12         System.out.println(numbers.removeLast());
13         System.out.println(numbers.removeFirst());
14         System.out.println(numbers.getFirst());
15         numbers.clear();
16         System.out.println(numbers.size());
17     }
18 }


Q3. What is the output after the following code is run?

 1 import java.util.LinkedList;
 2 
 3 public class MoreLinkedListQs {
 4     public static void main(String[] args) {
 5         LinkedList<String> countries = new LinkedList<String>();
 6         countries.addFirst("Canada");
 7         countries.addFirst("USA");
 8         countries.addLast("Thailand");
 9         countries.addLast("Malaysia");
10         countries.addLast("Madagascar");
11         countries.remove(3);
12         countries.add(2, "Ethiopia");
13         countries.addFirst("Zimbabwe");
14         countries.add(2, "Botswana");
15         for(int i = 0; i < countries.size(); i++){
16             System.out.println(countries.get(i));
17         }
18     }
19 }

.....

The following class shows the two different ways you can implement a List as a queue, and then the two different ways you can implement a List as a stack. This is good review of Topic 5, but also good practice for tracing.

List as Queue, with Adding First,
& List as Queue with Adding Last

First up, queue. Queue's just need to work in a FIFO way, so the removing and adding just need to be at opposite ends, so either adding first, or adding last works, as long as you remove from the opposite end.

 1 
 2 import java.util.LinkedList;
 3 
 4 
 5 public class MoreLinkedList {
 6     public static void main(String[] args) {
 7          listAsQueueAddingFirst();
 8          listAsQueueAddingLast();
 9          listAsStackUsingFirst();
10          listAsStackUsingLast(); 
12     }
14     /*
15      With stacks we work only at one end (be it "first" or "last"
16 
17      But with queues, we work with both ends (be it "add to first, and get from last"
18      or "add to last and get from first - which makes more sense.)
20     */
23     public static void listAsQueueAddingLast(){
24         LinkedList<Integer> intList = new LinkedList<Integer>();
25         intList.addLast(62);                       //62
26         intList.addLast(55);                       //62  55
27         intList.addLast(44);                       //62  55  44
28         intList.addLast(88);                       //62  55  44  88
29         intList.addLast(99);                       //62  55  44  88  99
//queue so remove from opposite end as added
30         System.out.println(intList.removeFirst());  //55  44  88  99    Output 62
31         System.out.println(intList.removeFirst());  //44  88  99        Output 55
32         System.out.println(intList.removeFirst());  //88  99            Output 44
33     }
34 
36     public static void listAsQueueAddingFirst(){
37         LinkedList<Integer> intList = new LinkedList<Integer>();
38         intList.addFirst(62);                       //62
39         intList.addFirst(55);                       //55 62
40         intList.addFirst(44);                       //44 55  62
41         intList.addFirst(88);                       //88  44  55  62
42         intList.addFirst(99);                       //99  88  44  55  62
//queue so remove from opposite end as added:
43         System.out.println(intList.removeLast());    //99  88  44  55    Output 62
44         System.out.println(intList.removeLast());    //99  88  44        Output 55
45         System.out.println(intList.removeLast());    //99  88            Output 44
47     }

List as Stack, Using Last/Last,
& List as Stack Using First/First

Next up, stack. And like queue, there are two ways to do it. But unlike queues both the removing and the adding will happen at the same end, whether working with the first or the last nodes; last/last or first/first.

48 
53     public static void listAsStackUsingLast(){
54         LinkedList<Integer> intList = new LinkedList<Integer>();
55         intList.addLast(62);                         //62
56         intList.addLast(55);                         //62  55
57         intList.addLast(44);                         //62  55  44
58         intList.addLast(88);                         //62  55  44  88
59         intList.addLast(99);                         //62  55  44  88  99
//stack so remove from same end as added
60         System.out.println(intList.removeLast());     //62  55  44  88    Output 99
61         System.out.println(intList.removeLast());     //62  55  44        Output 88
62         System.out.println(intList.removeLast());     //62  55            Output 44 
63     }
64 
65     public static void listAsStackUsingFirst(){
66         LinkedList<Integer> intList = new LinkedList<Integer>();
67         intList.addFirst(62);                         //62
68         intList.addFirst(55);                         //55  62
69         intList.addFirst(44);                         //44  55  62
70         intList.addFirst(88);                         //88  44  55  62
71         intList.addFirst(99);                         //99  88  44  55  62
//stack so remove from same end as added
72         System.out.println(intList.removeFirst());     //88  44  55  62    Output 99
73         System.out.println(intList.removeFirst());     //44  55  62        Output 88
74         System.out.println(intList.removeFirst());     //55  62            Output 44
75     }
76 }
77 

 

A copy and past of the Sample Paper question (page 46) which deals with lists.

 

D4.

(a) Award up to [3 marks max].
A queue is a first in first out structure;
Buses/objects should not be inserted in the middle of a queue;
Logically the first bus to leave/enter the queue will be the first to arrive/leave the queue;
Random access will not be required to a particular instance, making a queue more suitable than an array; [3 marks]

(b) Award marks as follows up to [3 marks max].
Award [1 mark] for three objects clearly representing a bus by some identifier (number or driver);
Award [1 mark] for objects in the correct sequence as represented by arrows

or otherwise;
Award [1 mark] for labeled start and end of queue;
Example diagram:

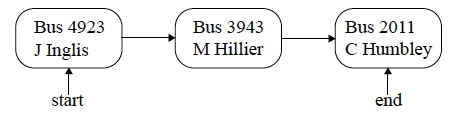[3 marks]

(c) Award marks as follows up to [4 marks max].
Award [1 mark] for correct return type of Boolean;
Award [1 mark] for correct test for pos less than queue size;
Award [1 mark] for correct test for pos > 0;
Award [1 mark] for correct return value;

Example answer:

private boolean removeBus(int pos){
    if ((pos < busQueue.size()) && (pos >= 0)){
        busQueue.remove(pos);
        return true;
    }
    else{
        return false;
    }
} 

[4 marks]

(d) Award up to [3 marks max].
A binary tree has pointers to left and right nodes;
Nodes can be ordered;
Such that smaller values are placed to the left/right of a node;
Which reduces search time;
To O(log(n)); [3 marks]