Sample Question:

sdfsdfsf

JSR Notes:

(A repeat from 5.1.7.) Firstly, remember that for Topic 5, "This will be examined at the level of diagrams and pseudocode.". But at the same time, remember that actual programmiing implementations will be necessary for the OOP Option.

In terms of whether or not you should, at this point, understand how the various methods work (pop( ), enqueue( ) etc.), it should not be necessary for Topic 5, but an appreciation of it at this point will help overall understanding of self referential systems, and the more sophisticated part of OOP. So it's worth looking at it ere. (*Though it's not so necessary for the class of 2021, with Paper 2 being dropped.)

 

Queue Algorithms

 

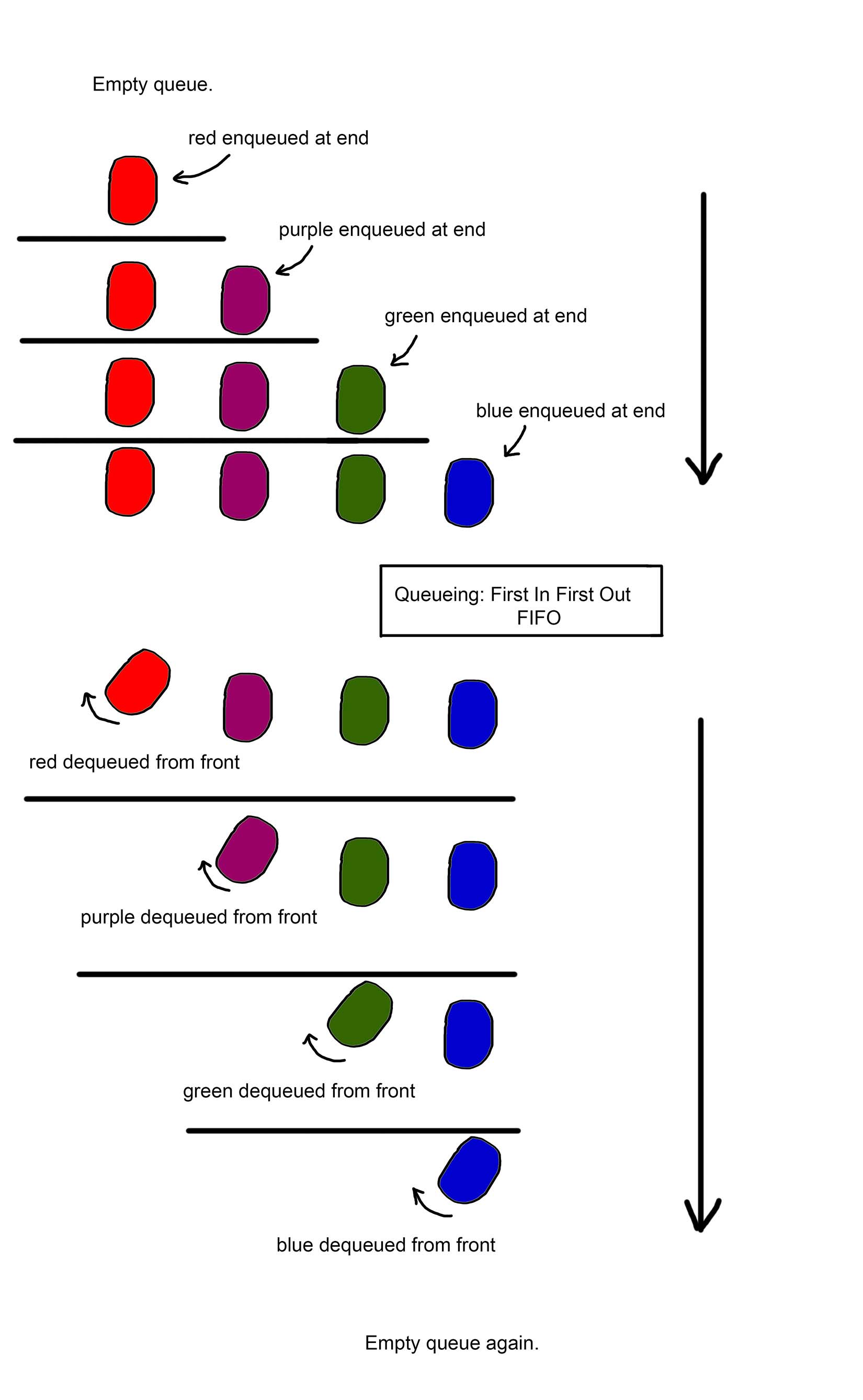
Remember that queues are lists that work in a First In, First Out (FIFO) manner. Note that for queues adding and taking away happen at OPPOSITE ends.

(And keep in mind stacking can work with head or tail, but it's LIFO that matters.)

 

Queuing Algorithm Functions
enqueue( ), dequeue( ), and isEmpty( )

 

Java Queue Algorithms Examples

public class MainForStacksAndQueues { 
    static LinkedList<String> listAsQueue = new LinkedList<String>(); 
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); 
 
    public static void main(String[] args) throws Exception{ 
        boolean keepAdding = true; 
        while(keepAdding){ 
            System.out.println("What do you want to add to the queue?"); 
            String s = br.readLine(); 
            listAsQueue.addLast(s); //so being built as a queue 
            System.out.println("Another item? true/false"); 
            keepAdding = Boolean.parseBoolean(br.readLine()); 
        } 
        if(!listAsQueue.isEmpty()) { 
            System.out.println("The first item to be dequeued off is: " + listAsQueue.removeFirst()); 
            //so taking the one that has been there the longest - thereby treating it in queue fashion 
        } 
 
        if(!listAsQueue.isEmpty()) { 
            System.out.println("The second item to be dequeued off is: " + listAsQueue.removeFirst()); 
        } 
    } 
}

IB Pseudocode Stack Algorithms Examples

queue LIST_AS_QUEUE
KEEP_ADDING = true

loop while KEEP_ADDING is true

output "What do you want to add to the queue?"
S = input
LIST_AS_QUEUE.enqueue(S)
output "Another item? true/false"
KEEP_ADDING = input

end loop

if not LIST_AS_QUEUE.isEmpty( ) then

output "The first item to be dequed off is" + LIST_AS_QUEUE.dequeue( )

end if

if not LIST_AS_QUEUE.isEmpty( ) then

output "The first item to be dequed off is" + LIST_AS_QUEUE.dequeue( )

end if

 

More Java Queue Tracing Examples

****Note that these examples are copied, pasted, and altered from D.4.12 for the no-OOP year 2021 only.

****Even though LinkedList doesn't have "enqueue( )", and "dequeue( )", I'll take the liberty to replace addFirst( ) and removeLast( ) with them in the queuing contexts below. (BTW, probably the reason the LinkedList class doesn't have "enqueue" and "dequeue" is because in the case of queues, "addLast", and "removeFirst" actually make just as much, if not more sense.)

 

Example - Straight-forward Queue Example

23     public static void queueExample(){
24         LinkedList<Integer> intList = new LinkedList<Integer>();
25         intList.enqueue(62);                       //62
26         intList.enqueue(55);                       //62  55
27         intList.enqueue(44);                       //62  55  44
28         intList.enqueue(88);                       //62  55  44  88
29         intList.enqueue(99);                       //62  55  44  88  99
30         System.out.println(intList.dequeue());      //    55  44  88  99    Output 62
31         System.out.println(intList.dequeue());      //        44  88  99        Output 55
32         System.out.println(intList.dequeue());      //            88  99            Output 44
33     }
34 


Q1. What is the output after the following code is run?

 1 import java.util.LinkedList;
 2 
 3 public class MoreLinkedListQs {
 4     public static void main(String[] args) {
 5         LinkedList<Integer> numbers = new LinkedList<Integer>();
 6         numbers.enqueue(99);
 7         numbers.enqueue(888);
 8         numbers.enqueue(11);
 9         System.out.println(numbers.dequeue());
10         numbers.enqueue(22);
11         numbers.enqueue(33);
12         System.out.println(numbers.dequeue());
13         System.out.println(numbers.dequeue());
14         numbers.enqueue(77);
15         numbers.enqueue(47);
16         System.out.println(numbers.dequeue());
17     }
18 }

Actual Ways Queues Work (more Option than Topic 5)

So here they are, in diagramatic and word form, he algorithms for queues. Remember that for queues, they always work in a First In First Out (FIFO) manner:

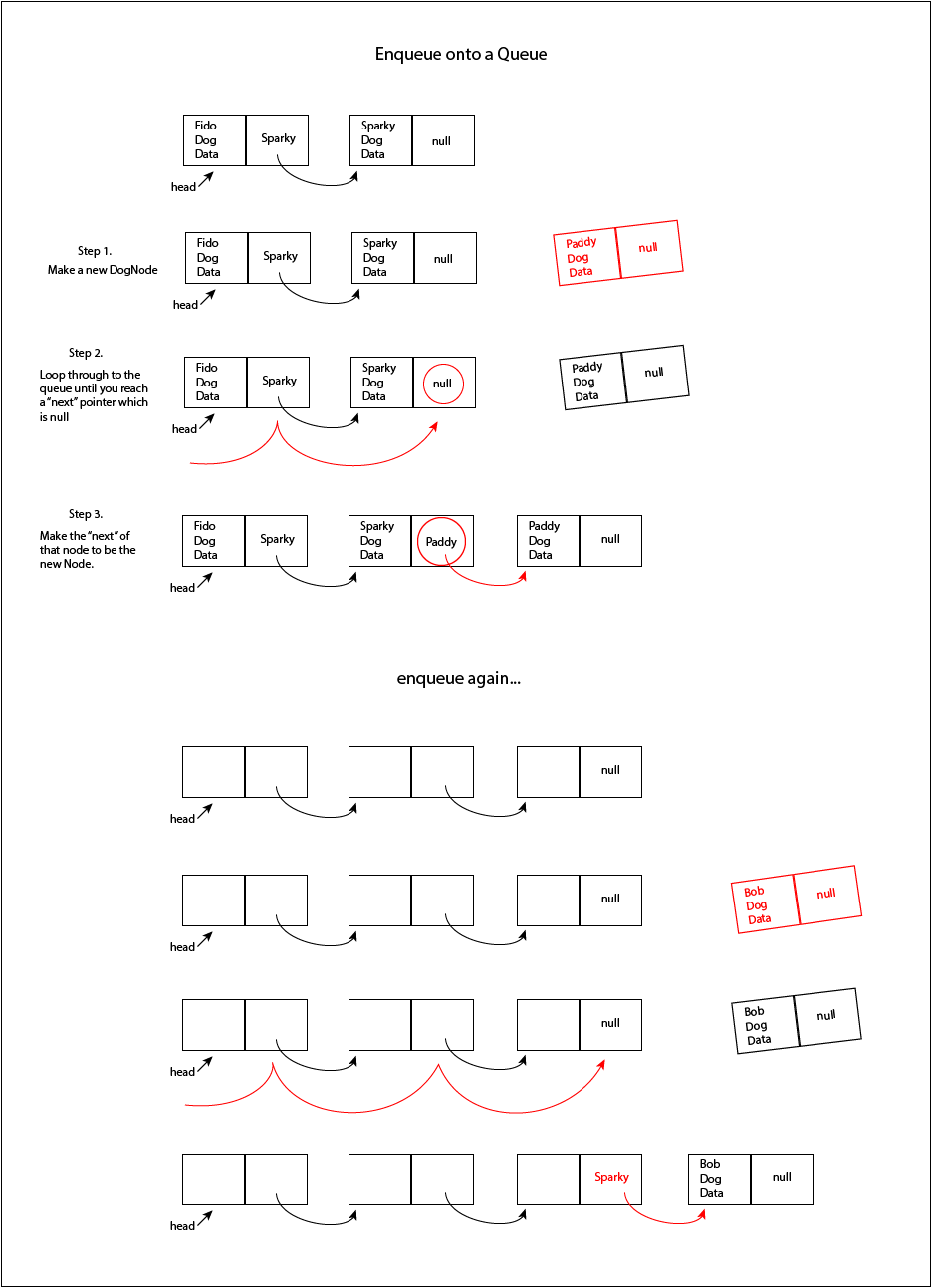
Enqueue onto a queue algorithm in words

• Make a new instance of the Node class.
• Starting at the head, iterate through the queue, one step at a time, until you reach the end (a node with next as null).
• Link that last node to the new node, by setting its next attribute to the new node.
• The new node is now linked at the end of the list.

 

 

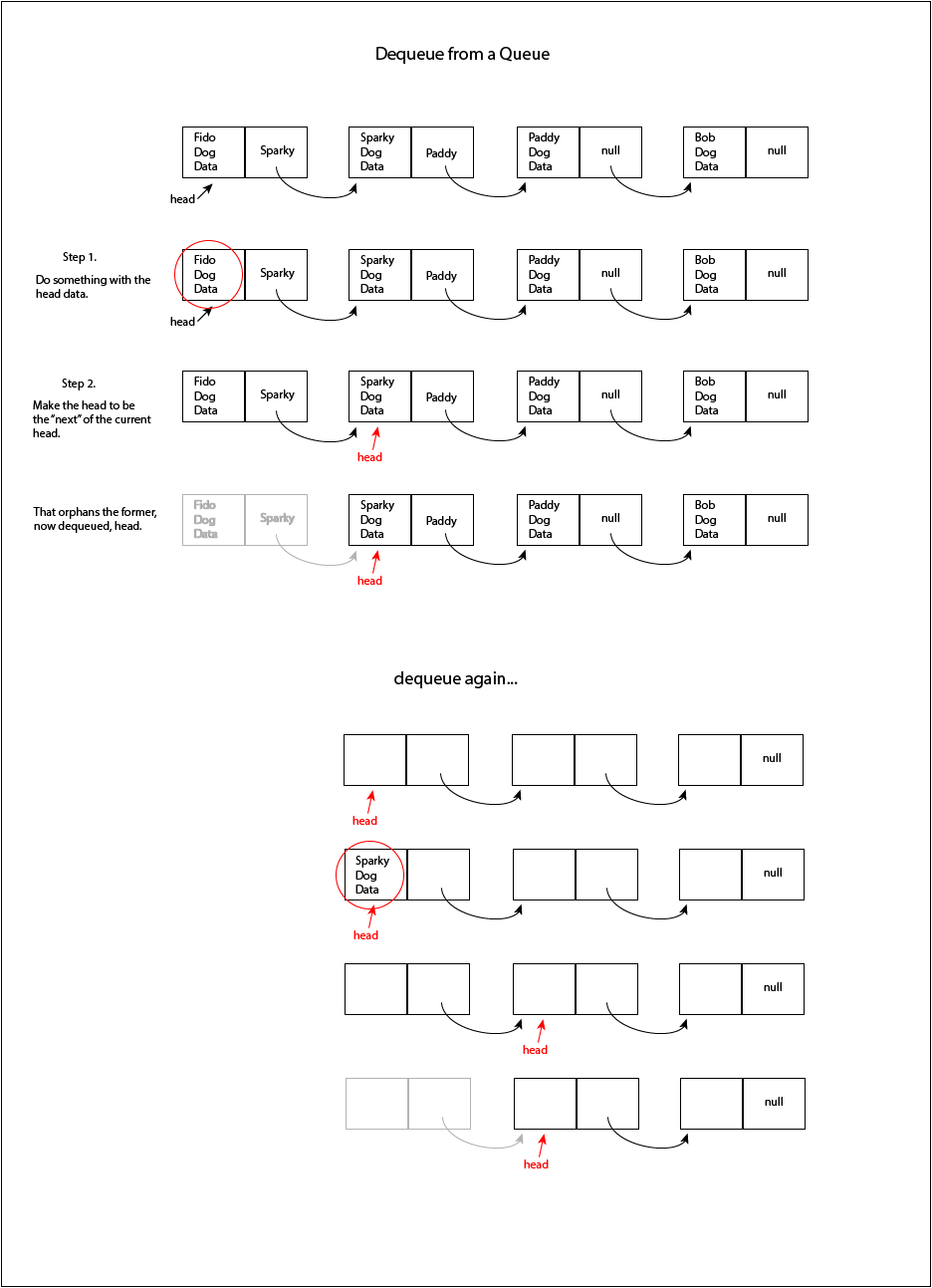
Dequeue from a queue algorithm in words

• Do something with the head data, like print it or assign it to a new Node variable.
• Make the head variable to be what the current head is pointing to (head = head.getNext( )).
• And that's it, the front data has been popped off, and the queue now starts at the former second node.

 

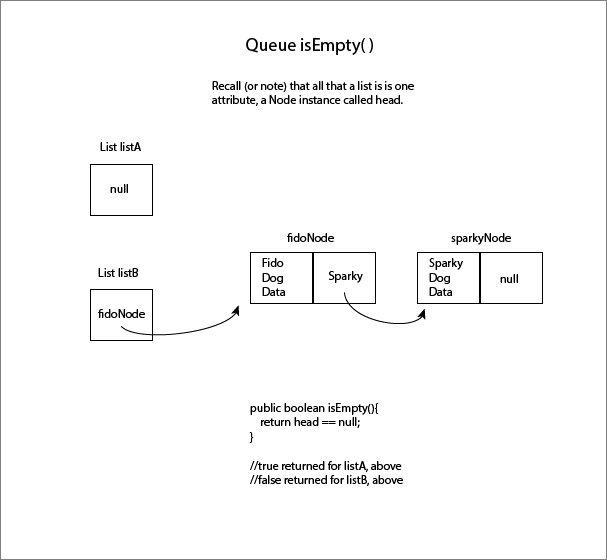
Queue isEmpty( ) in words

Recall that all a list is, is a Node attribute for keeping track of head. So, just like with a stack, for a queue, if that head attribute points to no head at all, i.e. it's head attribute is null, then isEmpty( ) returns false. Otherwise, it returns true.

 

Working with the head vs. the tail

Whereas the stack sets of diagrams mixed working with head and tail (the main ones, the head in both cases, and the optional ones with the tail in both cases), here, with the queue diagrams, both the main diagrams and the optional ones work the same way: adding at the tail, and removing from the head.

 

 

----------- OPTIONAL, AT LEAST HERE; ----------------

------------ THE OOP OPTION INCLUDES WORKING WITH TAILS ----------

 

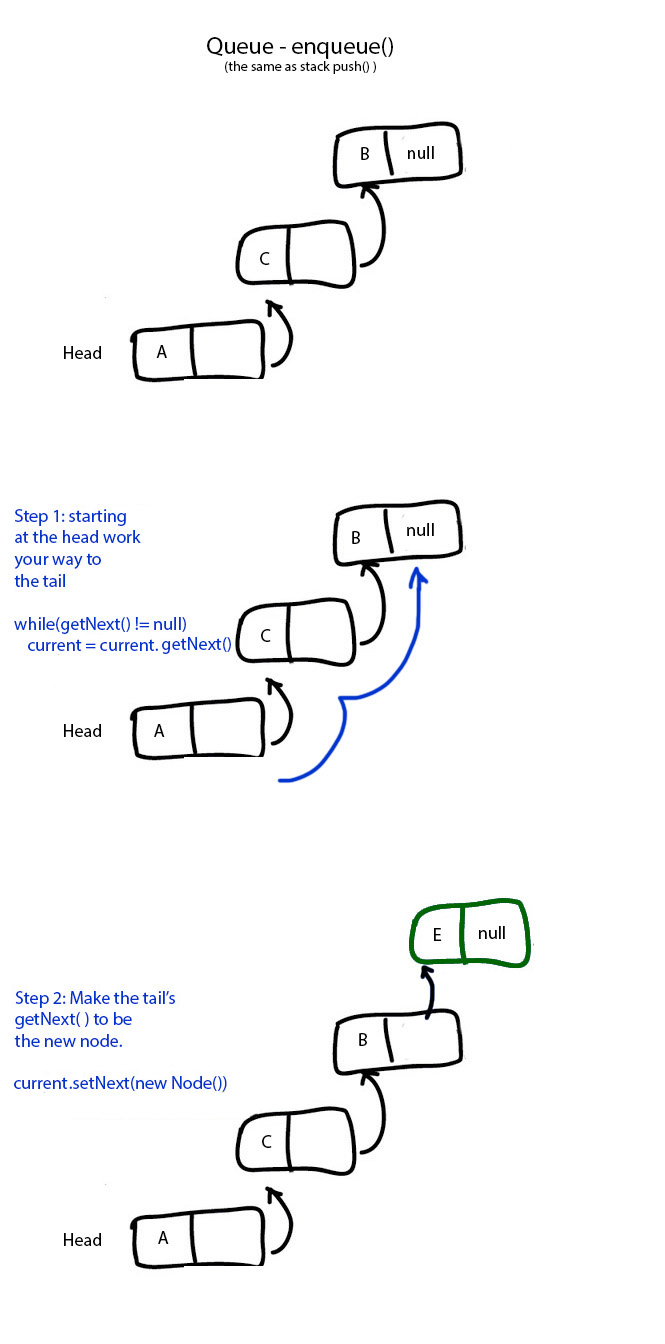
Queue Enqueue (to the tail) In Words

(Remember that this is exactly the same as a stack's push, just a different name with a different connotation; to a queue, say for example queue of students at the cafeteria check-out, you want to "enqueue" the latest student to what is effectively the end of the line.)

To start, remember that you can only ever access a list from the head; that is the only node that you have a record of via the list object itself - all the List object itself is is a reference address of the Head node.

So from the head, you make your way along the list, one step at a time, each step calling that node's getNext( ) function, which returns the address of the next node in the chain.

As soon as the getNext( ) you are at returns null, you know you are at the end of the list, i.e., the Tail. This is because only the Tail points nowhere. It is to the tail that you will "push" onto the stack your new Node.

So you make a new Node, and then have the Tail's setNext( ) function set the "next" to be the new Node. Keeping in mind that technically the new Node is an address. So now, that new Node is the last in the chain, able to be found all the way from the Head with a series of getNext( )s.

 

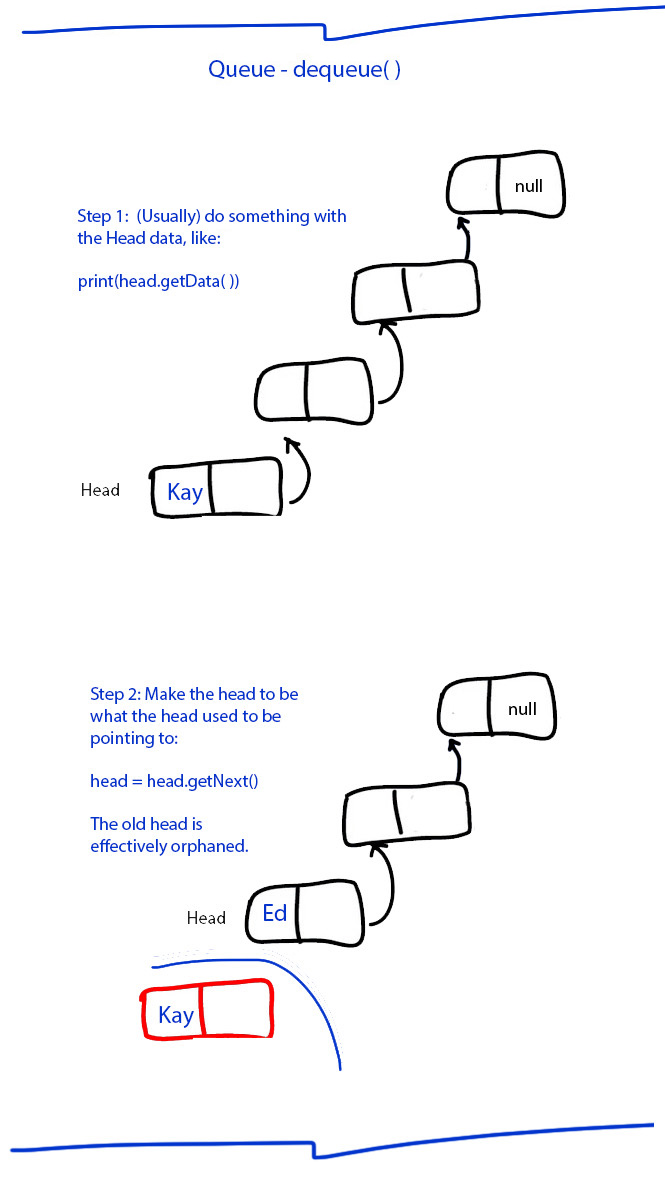
Queue Dequeue (from the head) In Words

Compared to the other stack/queue algorithms, this is the easiest, in that no traversal to the end of the List is needed. What we are looking to work with and remove from the List is actually the Head - the Node that has been there the longest.

So we first do what we want to do with the data at the Head, while we still have access to it - so for example print(Head.getData( ).getName( )).

And then we effectively orphan that Node by making the Head to be the Node that it is pointing to - i.e., the second in line, with (Head = Head.getNext( )).

Now the List, which ever only has direct access to the Head, can no longer work with the former Head; that Node has beed dequeued!

 

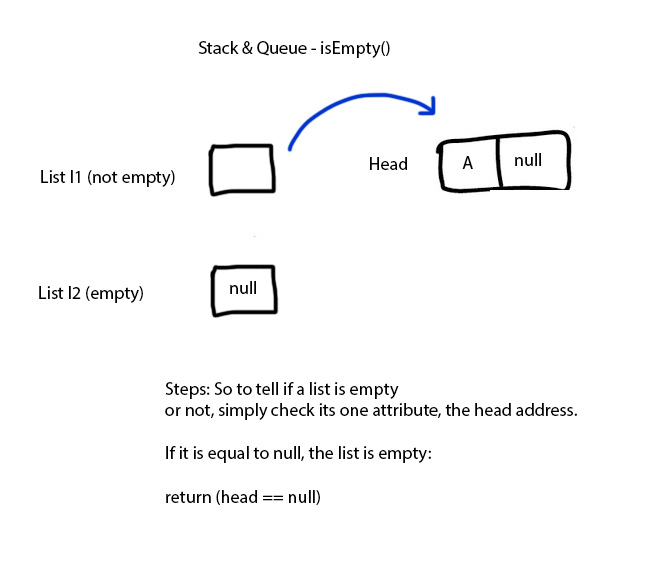
Queue isEmpty in Words

(This is the same for any list, including stack.)

Recall that as a data structure, a List is actually a reference type. And the address it keeps, that it references is the Head of the list. We will know that the List is empty is the Head is null.

In the above diagram, there are two situations; one in which there is a one-Node list; i.e. there is a Head, though nothing else. Note that this is not an empty list. And so, the List will indeed point to a Head. But in the empty list, the one and only pointer is null; in other words, the Head attribute of the List is null.

 

Re-cap

Below is a full movie of stacks and queues (using linked lists, which makes most sense). (This is the same one as in 5.1.7.) Note that I don't include an isEmpty method in the video. That would test to see if the head was == to null.

And also note that more Java implementation details are expected in the OOP extension later on in the curriculum.

Particularly, the enqueue( ) and isEmpty( ) methods are taken to a much deeper level in the OOP Option Extension later on in D.4.10.