Recursion Exercises

(These come from a textbook I used to use teaching AP CS, by Leon Schramm.)

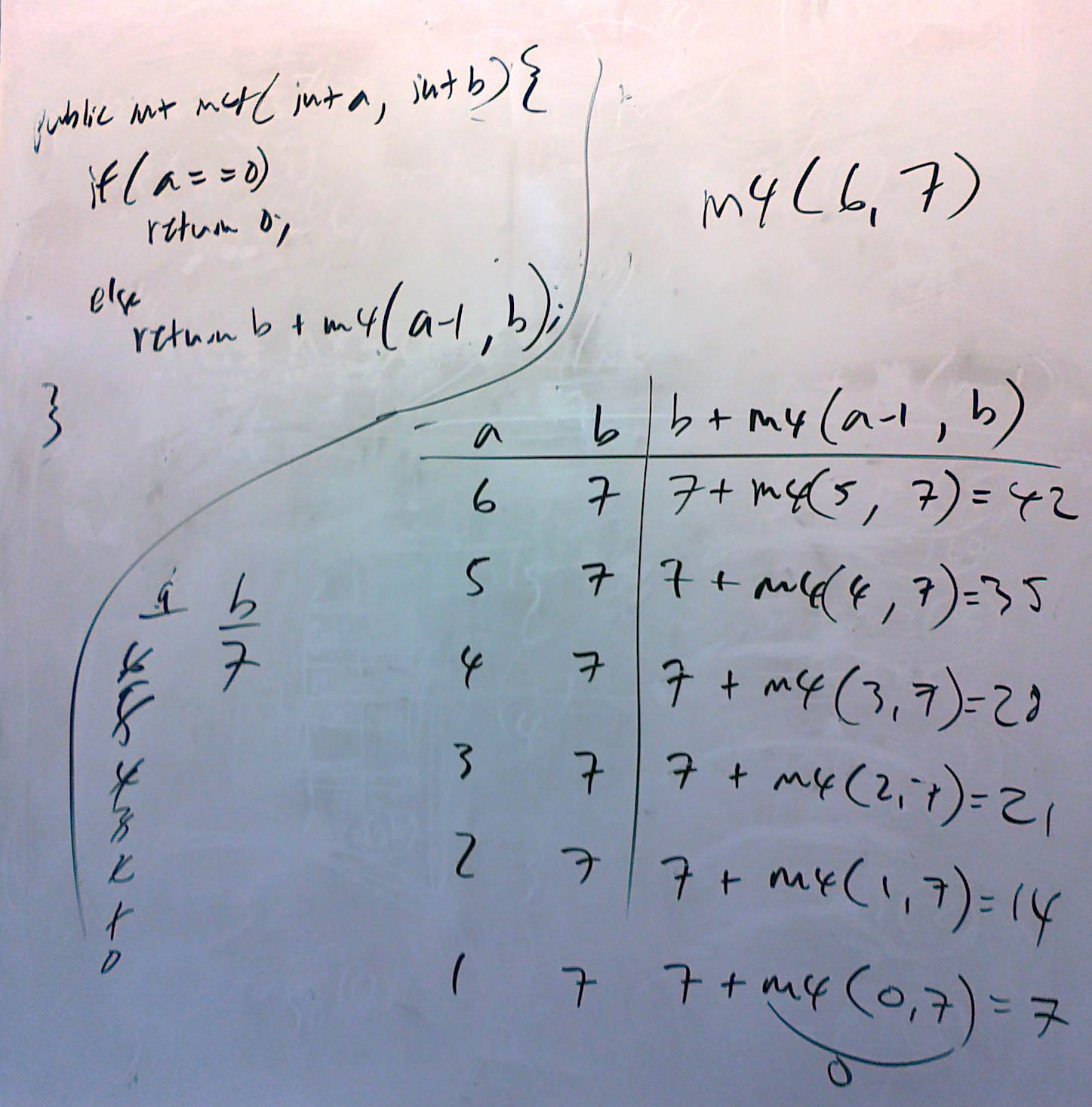
This is an image of the trace of exercise 9 below.

And here is a video showing how to do one of the exercises.

The idea is that when the first instance of the recursive method is called, the if condition is not true, so the method goes to the else block, in which another instance of the method is called. We show that in the trace table above as the call of m4(6, 7) is 7 + m4(5, 7). But we don't know what m4(5.7) is, since the "a" variable is still not 0. So another call to the m4 method is required, and so on, until, finally variable "a" is indeed 0, from which point we can work on up through the "stacked" calls.

6.
public int m1(int n)                                                              // m1(6) ==
{
   if (n == 1)
      return 25;
   else
      return n + m1(n-1);
}

 

7.
public int m2(int n)                                                              // m2(5) ==
{
   if (n == 5)
      return 0;
   else
      return n + m2(n+1);
}

 

8.
public int m3(int n)                                                              // m3(6) ==
{
   if (n == 1)
      return 1;
   else
      return n * m3(n-1);
}

 

9.
public int m4(int a, int b)                                        // m4(6,7) ==
{
   if (a == 0)
      return 0;
   else
      return b + m4(a-1,b);
}

 

10.
public int m5(int a, int b)                                                                //  m5(5,3) ==                 
{
   if (a == 0)
      return 1;
   else
      return b * m5(a-1,b);
}

 

11.
public int m6(int a, int b)                                                                // m6(3,5) ==
{
   if (b == 0)
      return 1;
   else
      return a * m6(a,b-1);
}

 

12.
public int m7(int a, int b)                                                                // m7(7,3) ==
{
   if (a < b)
      return 5;
   else
      return b + m7(a-1,b+1);
}

 

13.
public int m8(int n)                                                                                      // m8(6) ==
{
   if (n == 1 || n == 0)
      return 0;
   else
      return n + m8(n-1) + m8(n-2);
}