Binary Search Trees

& Linked Lists - The Basics

Back To RAM

Having spent the last few classes talking about how data can be saved permanently on storage devices such as hard drives, now we go back to the world of RAM. Since RAM is much faster at moving and changing data, there are many more algorithmic techniques that are possible; if they take many steps of processing, it doesn't matter, since those steps take place so quickly in RAM.

Arrays Are Static In Size

Up to now the only structure that you have worked with for storing multiple things is the array. And when an array in RAM is sorted, it makes searching very easy, since a binary search can be applied to it. So, fast searching is always possible with arrays in RAM. But there is one major disadvantage to arrays. The are static in size, or put another way, they are not dynamic. They cannot grow in size.

The Hap-hazard Way Memory Is Allocated

The reason is that memory gets allocated in a rather hap-hazard way around the RAM. Data continuously gets put into and taken out of RAM, and so even if we started writing from the first address, and just kept on filling in the RAM sequentially, as data gets swapped out of RAM, "holes" will appear back where we had already written stuff once. So in the middle of a work session, there are available chunks of RAM scattered all over the place. If we were to try to take an array in RAM and to "grow" it, it may or may not run into another area of RAM containing active data. But if it did run into other data it would over-write it, which would obviously be a bad thing.

Deciding On A Size For Your Array

When we declare an array of a certain type, we have to communicate to the computer the maximum number of those things that we will be working with. By doing a statement like int[] arr = new int[50]say, for example, "computer, reserve enough space for an array of 50 ints", so the computer finds 32 x 50 contiguous bits of memory in RAM and reserves those for the array, even if only a few of the elements get actually assigned anything. For arrays of only that many elements, it's not a big deal, but what if we made an array 1,000,000 chars, that would be 32 x 1,000,000 bits reserved. And if most of those bits remain unused, what a big waste of memory it is. But our strategy has to be to consider the worst case scenario of how many elements we will need to work with. Some times we are sure of the maximum number. For example, if we had an array of the days of the year we could be confident with an array of 366 elements (accounting for leap years.) But in most other cases, we will have to give ourselves a "cushion" of more elements than we will likely need, and so almost necessarily be wasting memory.

Binary Search Trees and Linked Lists To The Rescue

In computer science courses you always learn the array first because it's just more easy to learn, but in reality, with most groups of data you will have indefinite maximum numbers, so you'll use a binary tree. And in other cases you'll use linked lists. (It hasn't been mentioned yet, but in case you refer back to these notes later on, you would prefer a linked list over a binary search tree when you have data which should logically be accessed in either a stack way or a queue way. More on that shortly.)

In a nutshell, binary search trees are the Shangrila of structures that hold multiple things because they can be searched in a binary way, with similar efficiencies of the binary search of an array, and they also are dynamic, meaning that they can grow dynamically in size, and therefore not waste space.

Meantime, linked lists have an advantage over arrays in that they are dynamic data structures, yet they lack the array's advantage of having logarithmic search potential.

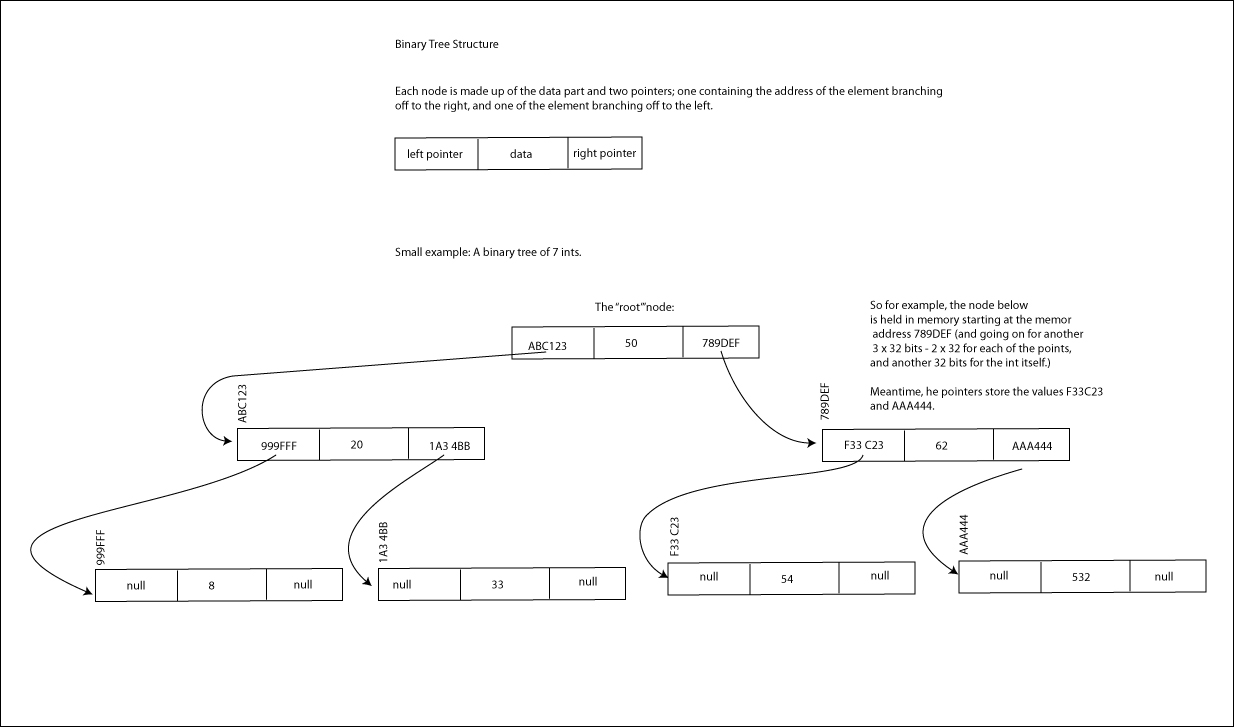
Binary Search Trees Basics

Sticking with "revolutionary" instructional sequence, here's the basic scoop about the binary tree. And that brings up a good initial point that "binary tree" is almost always referring to a "binary search tree"; it's just a shorter way of referring to it - and the point is that the ability to quickly search it is simplicity if it is organized in a binary tree way.

A binary tree is organized so that there is a "root" data element which has "descendants" added to the tree one at a time, which "branch" out from the root. New elements are added the the elements already in the tree based on whether they are "greater than" or "less than" the elements already there. A new element being added "moves" its way through the branches of the tree, at each node asking "Am I greater or lesser than this node?" If greater, it moves along the right branch, and if it is lesser it moves along the left branch. In this way it moves along branches until it gets to the end of a branch, where it is appended. "Greater" or "lesser" could mean in terms of numeric value, or it could mean in terms of alphabetical order, or some other kind of order.

Because of the tree structure, searching is done in a binarily efficient way as well. In searching for an element, we start at the root, and ask if the element we are looking for is greater than or less than the root, and then ask the same question at each node we get to as we work our way through the branches. At each node, we ask the same "greater than" or "less than" question, moving to the right if the answer is greater, and to the left if the answer is lesser, until we get to the element we are looking for. In a perfectly balanced tree, the maximum number of steps it will take to find any element of the tree is the log2N, with N the the number of elements. So for balanced binary tree of 1,000,000 elements, it would take 20 steps maximum to find an element. (The same number of steps as with a binary search.)

Meantime, because of the way a binary tree is built, there is no memory wastage. A binary tree only takes up as much space as there are elements, since they get added one at a time. So it is much more efficient than an array in this way. (There's a bit more to the story, as each element will need to also keep the address of the next elements which branched to the left and to the right, but those "pointers" are only 32 bit addresses.)

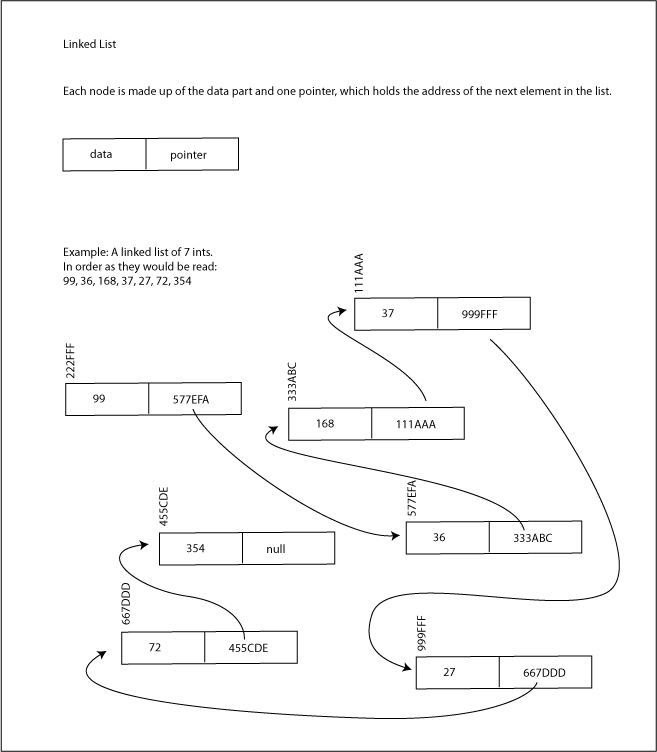
Linked List Basics

A linked list is a series of elements linked together in various places in memory. Unlike an array, whose elements are all next door to each other in memory (i.e. "contiguous"), the elements of a linked list are scattered through the RAM (just like with binary search trees). But each element knows where the next element "in the chain" is, by keeping track of the next element's memory address.

You can think of a linked list as being a binary tree with only one long twig that keeps on growing rather than branching. There is no logical binary structure, it is linear, with each element pointing to only one other.

But as with a binary tree, because the linking nature, no more memory is needed than for the current number of elements. In this way a linked list can grow, or in fact shrink, dynamically, without wasting memory.

And as in a binary tree, the elements keep track of the memory location of the next link by way of what's called a "pointer" - 32 bits of memory storing the address of the next link.